2.5. Проективное построение 4-ой гармонической точки
Упорядоченная четверка точек A, B, C, D прямой называется гармонической, если (ABCD) = –1. При этом точка D называется четвертой гармонической к точкам A, B, C.
Свойства. 1. " A, B, C Î $! D Î: (ABCD) =–1.
2. (ABCD) = –1 Þ (CDAB) = –1, (ABDC) = –1, (BACD) = –1.
3. Если C – середина отрезка AB, то четвертой гармоничной к ABC будет несобственная точка.
4. Для A, B, D¥ четвертой гармонической является середина отрезка AB.
Полным четырехвершинником наз. фигура, которая состоит из четырех точек расширенной плоскости, никакие три из которых не лежат на одной прямой, и шести прямых, которые про-ходят через все пары этих точек. Точки наз. вершинами, а прямые – сторонами четырехвершинника.
Стороны, которые не имеют общих вершин называются противоположными.
Точки A, B, C пересечения противоположных сторон называются диагональными точками, а прямые, которые проходят через пары этих точек называются диагоналями (AB, AC, BC).
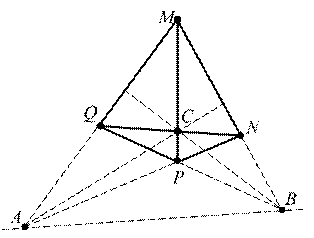
Рис. 8
Теорема. На каждой диагонали есть гармоническая четверка точек, состоящая из двух диагональных точек и двух точек пересечения этой диагонали со сторонами, которые проходят через третью диагональную точку.
Докажем, напр, что A, B, X, Y – гармоническая четверка (см. чертеж). Для этого спроецируем эти точки из точки N на прямую MP; получим M, P, C, Y. Затем спроецируем полученные точки из Q на прямую AB;получим B, A, X, Y.
Поскольку сложное отношение сохраняется при центральном проецировании, то (ABXY ) = (BAXY ) = Þ(ABXY )2 = 1Û(ABXY ) = ±1.
Но (ABXY ) = 1 Þ X = Y. Значит, (ABXY ) = –1.
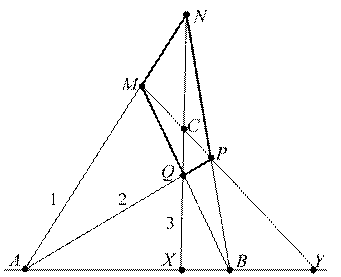
Рис. 9.
Эта теорема позволяет строить четвертую гармоническую точку.
Пусть даны точки A, B, X; требуется построить четвертую гармоническую к ним точку Y.
Строим
 2021-09-04
2021-09-04 403
403








