2021-09-04
34
Обозначение
цепей
Шаг tц,
мм
[Np] в кВт при
частоте вращения малой звездочки n1, об/мин
Передаточное отношение цепной передачи
iц = n1/n2 = ω1/ω2 = z2/z1 ≤ 7÷10. (7.7.1)
Передаточное отношение цепной передачи либо задается, либо рассчиты-вается по заданным частотам или угловым скоростям ведущей и ведомой звездочек согласно формулы (7.7.1).
Согласно рекомендациям табл.7.7.1 назначается число зубьев малой звез-дочки как среднее значение в зависимости от частоты вращения и передаточ-ного отношения – z1 = ƒ(n1) и z1 = ƒ(i). (7.7.2)
Число зубьев ведомой звездочки z2 = z1·iц ≤ zmax ≤ 120. (7.7.3)
Расчетная мощность проектируемой передачи (мощность, эквивалентная заданной, но учитывающая конкретные условия работы)
Np = N1/ kэ ≤ [Np], (7.7.4)
где N1 – задаваемая мощность передачи;
[Np] – табличное значение допускаемой расчетной мощности (табл.7.7.2);
kэ – коэффициент эксплуатации, учитывающий фактические условия
эксплуатации передачи.
Коэффициент эксплуатации
kэ=kд∙kа∙kα∙kрег∙kсм1∙kсм2• kz• kn, (7.7.5)
где kд = 1,0-1,8 – динамический коэффициент передачи (большие значения
принимаются при переменной нагрузке);
kа = 0,9-1,25 – коэффициент, учитывающий влияние увеличения Ац на
уменьшение износа цепи (при Ац ≈ (80÷20)∙tц);
kα = 1,0-1,25 – коэффициент, учитывающий влияние угла наклона α
оси между звездочками к горизонту (при 60º> α ≥ 60°);
kрег = 1,0-1,25 – коэффициент, учитывающий характер регулирования
провисания цепи (при регулировке с натяжкой звездочкой kрег = 1,0,
для нерегулируемых передач kрег = 1,25);
kсм1 = 1,0-1,5 – коэффициент сменности работы (в 1 смену – kсм1 = 1; в
2 смены – kсм1 = 1,25; в 3 смены – kсм1 = 1,5);
kсм2 = 0,8-1,5– коэффициент, учитывающий надежность смазки переда-
чи (регулярная смазка kсм2 = 0,8; без смазки kсм2 = 1,5);
kz – отношение табличного числа зубьев малой звездочки (табл.7.7.1) к
принятому для передачи (kz = k1табл / k1прин);
kn - отношение табличной частоты вращения малой звездочки
(табл.7.7.2) к заданной для передачи, по которой принимается
допускаемая мощность [Np] передачи.
|
Если при этом Np > [Np], то необходимо выбрать цепь с большим шагом или выбирается 2 х или 3 х рядная цепь и произвести предыдущие расчеты для цепи с новыми параметрами.
Оптимальное межосевое расстояние цепной
передачи Ац ≈ (30÷50)∙tц. (7.7.6)
Максимальное межосевое расстояние
Ацmax ≤ 80∙ tц. (7.7.7)
Диаметр делительной окружности звездочек
(мм) – рис7.7.5 D∂ = tц/sin(180/z). (7.7.8)
Допускаемое провисание холостой ветви цепи Рис.7.7.5. Схема сопряжения (мм) fц ≈ 0,02∙Ац. (7.7.9) роликов с зубьями звездочки
Натяжение цепи от центробежной силы (Н) Sv = q1∙υ2, (7.7.10)
где q1 – масса 1 го погонного метра цепи в кг (табл.7.7.3);
υ – линейная скорость цепи в м/с.
Линейная скорость цепи (м/c) υ = n1∙z1∙tц/(60∙1000). (7.7.11)
7.7.3.Некоторые характеристики приводных цепей
| Тип цепи | Шаг tц, мм | Вес q1, кг/м | Разрушающая нагрузка Ро, Н |
| 1.Втулочная (1 о рядная) | 9,525 | 0,44 | 11000 |
| 2.Роликовая (1 о рядная) | 8,00 9,525 12,70 15,875 19,05 | 0,18 0,41 0,60 0,80 1,52 | 4600 9000 18000 23000 25000 |
| 3.Зубчатая | 12,70 15,875 19,05 | 0,58 0,72 0,86 | 10000 12500 15000 |
Окружная сила на звездочках (H) Р = 1020• Nр/ υ. (7.7.12)
В цепных передачах иногда возникают резонансные явления, т.е. совпадение собственной частоты колебаний передачи с частотой возмущающих импульсов, что может вызвать нежелательную увеличенную амплитуду поперечных колебаний цепи. В связи с этим на этапе проектирования необходимо определить критическую частоту колебания передачи.
Критическая частота колебаний передачи (об/мин)
n1кр = 30∙√ Sв /q1/(z1∙Ац) < n1факт, (7.7.13)
где Sв – натяжение в ведущей ветви цепи (с незначительной погрешностью
можно принять Sв = P);
q1 –масса 1 го погонного метра цепи, кг;
Ац – межосевое расстояние, м;
z1 – число зубьев малой звездочки.
Если неравенство (7.7.13) не выполняется, то необходимо изменить пара-метры передачи и повторить предыдущие расчеты.
Периодически необходимо смещать подшипниковый узел вала со звездоч-кой, чтобы обеспечить оптимальное провисание цепи. В некоторых конструк-циях предусматривается натяжное устройство (подпружиненной звездочкой или планкой), компенсирующее вытяжку цепи (холостой ветви).
Основными критериями работоспособности цепных передач являются вытяжка шарниров цепи, раскалывание роликов и пластическая деформация (смятие) рабочих поверхностей зубьев звездочек (особенно с малым числом зубьев) по причине ударных нагрузок от неравномерности скорости ведущей ветви цепи.
Звездочки цепных передач изготавливают преимущественно из конструк-ционных среднеуглеродистых сталей обыкновенного качества и качественных сталей с термообработкой улучшение до НВ 310. Для высокоскоростных и тя-желонагруженных передач применяются качественные конструкционные сред-неуглеродистые стали с поверхностной закалкой до HRC 40…45.
Видеофильмы:http://www.youtube.com/watch?v=…
1…GVg9O9mFCs-Цепная передача. Анимация.
2…qDU7ly6Ku9o-Цепные передачи.
3…soZtaqo5SSE-Цепная передача.
Вопросы для самоподготовки:
1.Достоинства и недостатки цепных передач; области их применения?
2.Принцип выбора материалов для изготовления звездочек цепных передач?
3.Зачем необходимо натяжное устройство для цепной передачи (в особенности с большим передаточным отношением)?
4.Критерии работоспособности элементов цепной передачи?
5.Выбор межосевого расстояния цепной передачи?
6.Нужна ли смазка цепей передачи?
7.8. Передачи винт – гайка
Передачей винт – гайка называют механизм, состоящий из сопряжения винта и гайки, предназначенный для преобразования вращательного движения в поступательное (рис.7.8.1).
Передачи винт – гайка широко применяются в конструкциях различных устройств – винтовые домкраты, прессы с винтовым приводом ползуна, винтовые пары мерительного инструмента (микрометров), винтовая пара цепи резьбонарезания универсальных токарных станков и др.
|
|
- простота передачи (винт и гайка);
- большая несущая способность при ма-
лых габаритах;
- высокая точность перемещения (осо-
бенно при малых шагах резьбы);
- возможность обеспечения большого
выигрыша в силе.
К недостаткам можно отнести боль-
шие потери на трение и низкий к.п.д.
Для силовых передач применяют Рис.7.8.1. Схемы винтовой (а) и
упорные трапецеидальные или прямо- шарико-винтовой (б) передачи
угольные резьбы средних и крупных
шагов, для винтовых передач мерительного инструмента, делительных меха-низмов, в приборостроении - треугольные резьбы с малыми шагами. Винты не закаливаемые изготавливают преимущественно из среднеуглеродистых кон-струкционных сталей, закаливаемые – из пружинных сталей (HRC 40…50) или азотируемых cталей. Гайки изготавливают в основном из оловянистых бронз, а при малых скоростях и нагрузках из антифрикционных чугунов.
Передачи винт – гайка (в зависимости от назначения) выполняются:
- с вращающимся винтом и поступательно перемещающейся гайкой;
- с вращаюшимся и одновременно перемещаемым винтом и неподвижной
гайкой;
- с вращающейся гайкой и поступательно перемещаемым винтом.
Используются и другие схемы передачи движения.
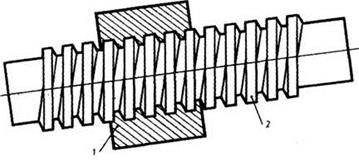
Передачи винт – гайка могут быть выполнены с использования принципа скольжения витков винта и гайки (рис.7.8.2, б) и принципа качения – в гайке и на рабочей поверхности винта изготавливаются винтовые дорожки (канавки) с полукруглым профилем, куда помещают шарики (рис. 7.8.2, а и рис.7.8.4).
|
|
|
|
|
|
Рис.7.8.2. Общий вид шарико-винтовой (а) и винтовой передачи (б)
Передаточное отношение механизма винт – гайка i = 1/p, (7.8.1)
где p – шаг резьбы (за 1 оборот винта (или гайки) гайка (или винт)
переместится в осевом направлении на один шаг в мм).
В силовых расчетах можно пользоваться зависимостью между окружной силой (Рм) на маховике (на ключе или рычаге), который вращает винт или гайку, и возникающей осевой силой на торце винта (Ро) или гайки (рис.7.8.3):
Ро = Рм· η ·π·Dм/р, (7.8.2)
где η – к.п.д. пары винт – гайка (в самотормозящих винтовых парах η< 0,5);
Dм – диаметр приложения силы на маховике;
р – шаг резьбы.
Коэффициент полезного действия винтовой пары
η = tg β/tg (β + ρ ), (7.8.3)
где β = arctg р/(π·d2) – угол подъема винтовой линии резьбы по средне-
му диаметру d2;
ρ = arctg (f/cosα/2) – приведенный угол трения в винтовой паре (здесь
f – коэффициент трения в винтовой паре, α – угол профиля резьбы).
Основные критерии работоспособности передач винт – гайка скольжения являются износ гайки и продольная устойчивость длинных винтов.
Средний диаметр резьбы d2 = √Pо/(π· ψн·ψh· [p]), (7.8.4)
где Pо – осевая сила на винте или гайке, Н;
ψн – коэффициент высоты гайки (для цельных гаек ψн = 1,2…2,5 и
для разъемных гаек – ψн = 2,5…3,5 – большие значения
принимают для резьб малого диаметра d2 ≤ 15 мм);
ψh – коэффициент формы профиля витка резьбы (для трапецеидальной
и прямоугольной резьбы ψh = 0,5, для упорной – ψh = 0,75, для
треугольной с α = 60° – ψh = 0,87);
[p] – допускаемое давление в паре виток винта – виток гайки (для матери-
алов пары не закаленная сталь – бронза [p] ≈ 9 МПа, закаленная сталь
– бронза [p] ≈ 12 МПа, не закаленная сталь – чугун [p] ≈5 МПа).
Передачи тяжело нагруженные проверяют на прочность по эквивален-тному номинальному напряжению
σэ = √(4·Pо/π·d12)2 + 3·(Mкр/0,1·d13)2 ≤ 0,3·σт, (7.8.5)
где d1 – внутренний диаметр винта, мм;
Mкр – момент кручения винта или гайки, Н·м;
σт – напряжения текучести материала винта, МПа.
Условие устойчивости длинных винтов (рис.7.8.3)
Pо ≤ π2·Е·J/ ((n· (μ·ι)2 ), (7.8.6)
где Е = модуль упругости материала винта (Е = 2,1· 105 МПа);
J = π·d14·(0,4 + 0,6·d/d1)/64 – приведенный момент инерции сечения
винта (здесь d – наружный диаметр винта, d1 – внутренний), мм4;
 
 
  
  
  
|
|
опорами; для винтов с одной опорой и гайкой –
расстояние между опорой и серединой гайки, мм;
μ·ι ≥ 25·d1 – приведенной длина винта выше гайки;
n = 2,5 – 4,0 – коэффициент безопасности передачи,
зависящий от степени ответственности передачи,
режима и неравномерности нагружения винта
В механизмах точных силовых перемещений широко
применяются винтовые передачи качения применяют
(приводные механизмы перемещения рабочих органов Рис.7.8.3.Схема нагру-
металлорежущих станков, следящие системы радиоло- жения длинных винтов
каторов, ответственные силовые передачи и др.).
Конструкция пары винт – гайка качения показана на рис.7.8.4, а, б. Винто-
вые поверхности могут быть однозаходные и многозаходные. Винтовые ка-навки закаливают до твердости HRC 60…63 и азотируют. Гайки и шарики из-
|
готавливают из шарикоподшипниковых или цементу-
емых сталей с закалкой. Диаметр шариков принима-
принимают dш ≈0,6·р. Допускаемое контактное нап-
ряжение выносливости принимают [σк] ≈ 2500…
3000 МПа. Усилие на шарик F1 ≈ 2·dш2.
Общая допустимая осевая нагрузка на винт (или
гайку) Ро = zp· F1·sin α·cos β, (7.8.6)
где zp = 0,7·z – расчетное число шариков (здесь
z –число шариков, находящихся в контакте Рис.7.8.4.Шариковая пара
винт - гайка); винт – гайка качения
α = 45° - угол контакта шариков в сопряжении (рис.7.8.4, а, б);
β = arctg р/(π·d2) – угол подъема винтовой линии резьбы по средне-
му диаметру резьбы.
Видеофильмы: http://www.youtube.com/watch?v=…
1…C-ksyfnVPig-Шарико-винтовой привод станка.
2…XgJziykGqw-Шарико-винтовая передача.
3…b0pDJSC0xNE-Винты для ШВП.
4…еUwplZslBFY-Фланцевая гайка (ШВП).
5…eGM3QleZHdg-Шарико-винтовая передача. Сборка.
Вопросы для самоподготовки:
1.Назначение передач винт – гайка? Их достоинства и недостатки?
2.Какие материалы применяются для изготовления винтов и гаек в передачах
скольжения и качения?
3.Критерии работоспособности и основы расчета передач винт – гайка
скольжения?
4.Зачем необходим расчет на устойчивость длинных винтовых передач?
5.Основы расчета допустимой осевой нагрузки винтовых элементов передачи винт – гайка качения?
7.9. Фрикционные передачи
Фрикционной называют передачу, в которой передача и преобразова-ние движения основана на использовании сил трения сцепления, возни-кающих в месте контакта, как правило, вращающихся тел под действием сжимающих сил (рис.7.9.1).
Фрикционные передачи могут быть нерегулируемые, т.е. с неизменным пе-редаточным отношением (рис.7.9.1, а, б, в), и регулируемые, т.е. с возможнос-тью бесступенчатого изменения передаточного отношения – вариаторы (рис.7.9.1, г, д).
|
Передаточное отношение фрикционных передач
i = n1/n2 = D2/(D1·(1 - ε)), (7.9.1)
где n1и n2 – соответственно частоты вращения ведущего и ведомого катков
или шкивов (или валов, на которых они установлены);
D1 и D2 – соответственно диаметры ведущего и ведомого катков или
шкивов;
ε ≈ 0,01…0,03 – коэффициент проскальзывания сопрягаемых поверх-
ностей.
Сила прижатия цилиндрических катков для обеспечения необходимой окружной силы Ft или крутящего момента
Q = kз· Ft/f, (7.9.2)
где kз ≈ 1…3 – коэффициент запаса сцепления (бόльшие значения прини-
маются в приводах приборов и при значительных колебани-
ях потребляемой нагрузки);
f – коэффициент трения сцепления материалов пары сопряжения.
В зависимости от сочетания материалов сопрягаемых поверхностей тел передачи коэффициент трения принимают:
- сталь по стали в масле f ≈ 0,04…0,05;
- сталь по стали или чугуну без смазки f ≈ 0,15…0,20;
- сталь по текстолиту без смазки f ≈ 0,2…0,3;
- фрикционный пластик по резине f ≈ 0,4…0,5;
Сила прижатия конических катков для обеспечения необходимой окружной силы Ft или крутящего момента
Q = kз· Ft·sin(α/f), (7.9.3)
где α – половина угла конуса катка.
Фрикционные передачи (в основном регулируемые) широко применяются в приводах контрольно-измерительной аппаратуры, намоточных станков прибо-ростроителных, текстильных и иных предприятий, силовых приводов механи-ческих прессов, легковых автомобилей, квадроциклов и др. машин. Принцип работы клинового вариатора (рис.7.9.2, д) – при раздвигании и одновременном сдвиге ведущих и ведомых пар конусов (полушкивов) обеспечивается переме-щение клинового широкого ремня на другие рабочие ди аметры, что и изменяет передаточное отношение. В лобовом вариаторе (рис.7.9.1, г) перемещение ведущего катка вдоль оси вала изменяет диаметр его сопряжения с катком ведомого вала, а, следовательно, и передаточное отношение.
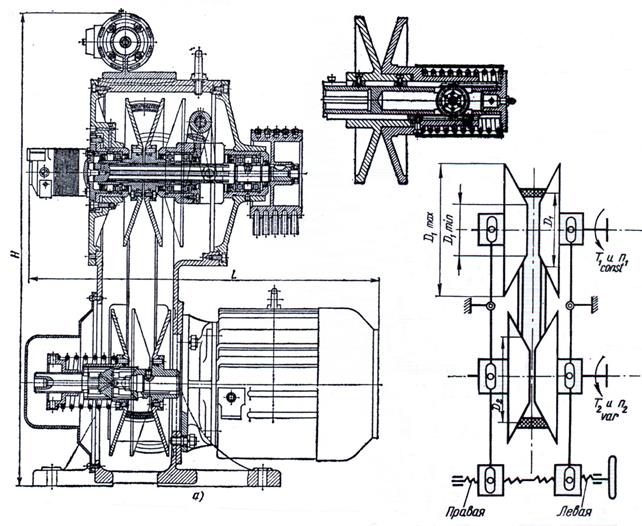
Рис.7.9.2. Конструкция (а) и схема (б) клиноременного вариатора с
раздвижными шкивами
Максимальное передаточное отношение в силовых вариаторах редко превы-шает 4…8 (к.п.д. 0,9…0,7), а в намоточных устройствах иногда достигает и 25.
Основные недостатки фрикционных передач:
- наличие скольжения в сопряжении фрикционных тел и их повышенный износ;
- некоторое непостоянство передаточного отношения, что, в ряде случаев,
- ограничивает их применение в передачах кинематического назначения;
- пониженный к.п.д. по причине потерь на скольжение и повышенных усилий в
опорах валов.
Достоинства фрикционных передач:
- возможность бесступенчатого регулирования передаточного отношения;
- относительная простота конструкции.
Видеофильмы: http://www.youtube.com/watch?v=…
1…vfUb6VH0Kwmg-Как работает вариатор. Анимация.
2…XW2KYir-lE-Фрикционные передачи и вариаторы.
3…yLrJlLG09ë-Как работает вариатор.
4…fZQi4a3lro8-Принцип работы вариатора. Анимация.
Вопросы для самоподготовки:
1. Каков принцип работы фрикционных передач?
2. Как можно определить передаточное отношение фрикционной передачи?
3. Зачем нужно прижимать тела сопряжения друг к другу?
4. Каким образом можно снизить проскальзывание в передаче?
8. Валы и оси. Расчет валов и осей
а. Общие вопросы
Валы – стержневые детали, служащие для установки на них других деталей (зубчатых колес, шкивов, звездочек, дисков, рычагов и др.) и передачи движения в пространстве, а также для обеспечения необходимого положения в пространстве установленных на них деталей.
В свою очередь валы устанавливаются на опоры (например, в подшипники, на призмы и др.), что и обеспечивает их требуемое положение в пространстве.
Валы передают крутящий момент и совершают вращательное движение или вращательно-колебательное.
|
Оси, в отличии от валов, не передают крутящий момент и могут вращаться или быть неподвижными.
По прямолинейности осей валы
подразделяются на (рис.8.1):
а – с прямолинейной осью (прямые);
б – коленчатые (с коленообразной осью);
в – гибкие валы (с криволинейной осью
и могут изгибаться).
Наибольшее применение находят Рис.8.1. Разновидности валов по пря-
валы с прямолинейной осью (валы ре- молинейности их осей: а - с валы с
редукторов, коробок скоростей, бараба прямолинейной осью; б- коленчатые;
нов подъемных механизмов и др.). в- с криволинейной осью.
Широко используются и коленчатые валы (в двигателях внутреннего сгорания, механических прессах, швейных машинках и др.). Реже используются гибкие валы (гибкий вал бормашинки зубного кабинета, борма- шины для ручной гравировки, механизм привода тахометра двигателя и др.).
По конструктивным особенностям валы и оси бывают:
- гладкие (имеют одинаковое сечение по всей длине) – рис.8.2, а;
- ступенчатые – рис.8.2, б;
- сплошного сечения (отсутствуют осевые отверстия) – рис.8.2, а, б;
|
- полые (со сквозным отверстием) – рис.8.2, в
Валы и оси изготавливаются из:
- среднеуглеродистых сталей обыкновенного
качества (Ст.4; Ст.5) без термообработки или
с улучшением (для неответственных и мало-
нагруженных узлов и с небольшими частота-
ми вращения); Рис.8.2.Конструктивные осо-
-среднеуглеродистых качественных (Сталь 35; бенности валов: а- гладкие;
Сталь 40; Сталь 45) и низколегированных б - ступенчатые; в – полые
сталей (Сталь 35ХН; Сталь 40Х и Сталь 40ХН; Сталь 45Х и др.) с термообра- боткой «улучшение» (для узлов средней нагруженности и при средних частотах вращения);
- низкоуглеродистых легированных цементуемых сталей (Сталь 20; Сталь 20Х; Сталь 18ХГТ и др.) – для коробок скоростей и др. ответственных узлов (с цементацией и закалкой поверхностей под подшипники или другие устанавливаемые на него детали).
Расчет валов производят на:
1. Статическую прочность (проектный расчет).
2. Усталостную прочность (проверочный расчет).
3. Жесткость (изгибную или крутильную – проверочный расчет).
4. Виброустойчивость (проверочный расчет).
Кроме этого, производится оценочное сопоставление рассчитанных диа-метров валов в сечениях опор по критериям работоспособности устанавли-ваемых на них подшипников.
Конечной целью расчета является назначение материала вала, его терми-ческой обработки и получения геометрических параметров вала, достаточных для его проектирования и обеспечения необходимой эксплуатационной надежности и долговечности работы.
б. Расчет валов на статическую прочность (проектный расчет).
При этом должны быть известными передаваемый валом (или на вал)
крутящий момент Мкр и изгибающие моменты Ми в сечениях вала, частота вращения n (если известна мощность N и угловая скорость ω или частота вращения вала n, то Мкр= 9555·N/n=2π·9555·N/ω), размеры насаживаемых на вал деталей, точки приложения, величины и направления действующих на них сил или моментов сил.
Однако изгибающие моменты в сечениях вала невозможно определить пока не будут найдены реакции в опорах и расстояния между расчетными сечениями вала, а вышеназванные расстояния – пока не определены линейные размеры опор (например, ширина подшипников), а размеры опор – пока не найдены реакции в опорах, т.е. возникает заколдованный круг.
Поэтому в инженерной практике поступают следующим образом:
1. Назначается материал вала и его термическая обработка с учетом экс-плуатационных требований – степень нагруженности, долговечность работы, ответственность изделия, условия работы и др. 0 1 2 3
2. Вычерчивается расчетная схема узла ва-
ла без простановки осевых размеров – рис8.3.
3. Определяются расчетные сечения вала: 
Мкр Fr Ft
0-0 – свободный конец вала, на который ус- 0 1 F0 2 3
танавливается какая- либо деталь (полумуф- Рис.8.3. Расчетная схема узла вала:
та, зубчатое колесо, звездочка и др.), дейст- 0-0, 1-1, 2-2, 3-3 – расчетные сече-
вует крутящий момент Мкр; сечения, напри- ния; F0, Ft, Fr –действующие силы,
мер,1-1 и 3- 3 установки подшипников; 2-2 - приложенные к насаженной сечение установки на вал какой- либо детали на вал детали
(зубчатое колесо, звездочка, барабан и др.) и к которой приложены внешние силы (в точке симметрии). Устанавливаемых на вал деталей может быть и больше – расстояние между ними считаются уже известными.
4. Производится расчет диаметров вала в расчетных сечениях по понижен-
ным напряжениям кручения (что компенсирует в определенной степени незна-
ние точных величин изгибающих моментов и их влияние на диаметр сечений).
Диаметры вала (мм) в рассматриваемых сечениях рассчитываются по формуле: di=10 3√ Мкр/(0,2·[τ]кр), (8.1)
где Мкр – величина крутящего момента в сечении (на отрезке между
сечениями 0-0 ÷ 2-2 Мкр – const, а 2-2 ÷ 3-3 Мкр= 0 – рис.8.3),Н·м;
[τ]кр – допускаемые напряжения кручения материала вала, МПа.
Допускаемые напряжения кручения (по сердцевине вала) принимаются:
- для валов из среднеуглеродистых сталей обыкновенного качества типа Ст.4, Ст.5, Ст.6 с термообработкой (Т.О.) улучшение НВ 190…230 -[τ]кр≈13÷22 МПа;
- для валов из среднеуглеродистых качественных сталей типа Сталь 40, Сталь 45 с Т.О. улучшение НВ 230…270 - [τ]кр≈15÷25 МПа;
- для валов из среднеуглеродистых низколегированных сталей типа Сталь 35ХН, Сталь 40Х, Сталь 40ХН с Т.О. улучшение НВ 230…270 - [τ]кр≈17÷28 МПа;
- для валов из цементуемых легированных сталей типа Сталь 20Х, Сталь 12ХНЗА, Сталь 18ХГТ и др. с Т.О. улучшение до 190…200, цементацией на глубину 0,8÷1,2 мм (отдельных поверхностей) и закалкой HRC 57…62 -[τ]кр≈20÷30 МПа.
Для сечений, в которых действует только крутящий момент (например, в
сечении 0-0 - рис.3) принимается бо'льшая величина [τ]кр из рекомендуемого диапазона, для сечений установки подшипников (сечения 1-1 и 3-3) прини-маются средние величины [τ]кр диапазона, для сечений, в которых действуют максимальные величины крутящего и изгибающего моментов (например, сечение 2-2) принимаются меньшие значения диапазона напряжений.
Найденные диаметры валов в сечениях установки подшипников округ-ляются до ближайшего большего или меньшего значения диаметра внутрен-него кольца выбираемого типа стандартного подшипника. Диаметры валов в левой и правой опоре принимают чаще всего одинаковыми с целью унифи-кации подшипников (если последующий расчет подшипников подтвердит правомочность этого допущения). Валы проектируются преимущественно ступенчатыми. Разница диаметров ступеней в сечениях 0-0 и 1-1 ≥1-3 мм, в
сечениях 1-1 и 2-2 ≥3-8 мм с целью обеспечения достаточной площади тор- цевой опорной поверхности. Диаметр опорного фланца вала под устанав-ливаемую деталь dф ≥d2 + 3f (f – фаска или галтель в отверстии детали). Диа-метры валов в сечениях 0-0 и 2-2 округляются до большего или несколько меньшего целого числа. Величины фасок или радиусов галтелей в сопряжении можно принимать f (Rг) ~(0,035÷0,04)•di, а радиус галтели вала в сопряжении с подшипником Rг < радиуса галтели r подшипника (di – диаметр вала в сечении).
5.Фиксируется тип и номер выбранных подшипников и записываются их размеры: d·в·Д·r =……мм согласно соответствующего ГОСТ на подшипник, а также его статическая С0 и динамическая Сд грузоподъемности (d –диаметр отверстия внутреннего кольца, Д – диаметр наружного кольца, в – ширина и r –радиус галтелей подшипника).
   
|
6.Проектируется конструкция узла вала (рис.8.4). Диаметры сечений вала определены в п.4. Осевые размеры при установке узла вала, например, в корпус редуктора (ориентировочно):
k ≈ (3 ÷ 4)*впi; (8.2)
h1≈2÷3 мм и h2≈5÷10 мм; (8.3)
а ≈ впi/2+h1+h2+ вд/2; (8.4)
б ≈ вд/2+h1+h2+вп/2, (8.5)
где h1 – предпочтительное рас-
стояние от торца подшипника
до внутреннего края корпуса;
k – расстояние от левого торца
вала до середины ширины под- Рис.8.4.Схема конструкции узла вала:
шипника (3..4•d0); 1- вал; 2 - подшипники; 3 - корпус
h2 – зазор между торцем ступицы редуктора; 4 – шестерня.
насаженной детали и краем корпуса;
Вд – ширина насаженной детали.
7. Формируется расчетная схема узла вала с установленными расстояниями между сечениями – рис.8.5 – и определяются реакции в опорах, изгибающие
моменты в расчетных сечениях и строятся эпюры изгибающих и крутящих моментов от действующих сил.
Расчетная схема узла вала (рис.8.5,а) является моделью конструкции вала. В связи с этим расчет становится несколько приближенным. Для вращающихся валов используют в основном 2 типа опор: шарнирно-неподвижную (например, левая опора) и шарнирно-подвижную (правая опора). Шарнирно-неподвижная опора воспринимает радиальную и осевую нагрузки, а шарнирно-подвижная – только радиальную. Силы, приложенные к насаживаемой детали, представляют как сосредоточенные в каком-либо сечении.
Перенесем действующие на насаживаемую деталь силы на ось вала и деталь
не будем учитывать в расчете (рис.8.5,б).
Определение реакций в опорах и действующих изгибающих моментов в рас-
расчетных сечениях вала производят отдельно в вертикальной (рис.8.5, в) и го-
ризонтальной (рис.8.5, г) плоскостях, а затем рассчитывают их суммарные зна-
чения (посредством геометрического сложения). Условно подшипники заменя-ем реакциями в опорах – при этом вся система – узел вала – остается в состоя-нии равновесия.
При расчете реакций в опорах и изгибающих моментов в сечениях вала действующие внешние силы и моменты принимаются известными (они рассчи-тываются заранее).
В расчетах необходимо принять: вектор моментов действующих сил, нап-равленный «по» часовой стрелке, с +, а против – с – (или наоборот). Векторы реакции в опорах направляют против векторов действующих сил или моментов (если это видно явно на расчетной схеме, если не видно – в любую сторону). Знак – будет свидетельствовать, что фактическое направление вектора реакции – в обратную сторону). Эпюры изгибающих моментов строятся без масштаба на сжатых или на растянутых волокнах.
|
1.Расчет реакций в опорах и моментов сил в вертикальной плоскости
(рис.8. 5,в):
- момент от переноса осевой силы Fo с детали к оси вала: Мo=Fo*Дд/2; (8.6)
-сумма моментов действующих сил и момента Мo относительно левой опоры L:
ΣМлв=Мo-Fr·a+Rпв·(а+б)=0, (8.7)
откуда реакция в правой опоре: Rпв=(Fr·a-Мo)/(а+б). (8.8)
Примечание. Моменты сил F0 и Rлв равны 0, т.к. векторы сил проходят
через ось опоры.
- осевая реакция А в левой опоре: А=F0; (8.9)
- сумма моментов действующих cил относительно правой опоры П:
ΣМпв=М0+Fr·б-Rлв·(а+б)=0, (8.10)
откуда реакция в левой опоре Rлв=(М0+Fr·б)/(а+б); (8.11)
- изгибающий момент в сечении 2-2 (от сил слева): Мв2л=-Rлв·а; (8.12) - изгибающий момент в сечении 2-2 (от сил справа): Мви2п=Rпв·б. (8.13)
2.Расчет реакций в опорах и моментов сил в горизонтальной плоскости (рис. 8.5,г):
- сумма моментов действующих сил относительно левой опоры L:
ΣМлг= Fм·k-Ft·a+Rпг·(а+б)=0, (8.14)
откуда реакция в правой опоре: Rпг=(-Fм·k+Ft·a)/(а+б); (8.15)
- сумма моментов действующих сил относительно правой опоры П:
ΣМпг= Ft·б-Rлг·(а+б)+Fм·(а+б+k)=0, (8.16)
откуда реакция в левой опоре: Rлг=(Ft·б+Fм·(а+б+k))/(а+б); (8.17)
- изгибающий момент в сечении 1-1: Мги1= Fм·k; (8.18)
- изгибающий момент в сечении 2-2: Мги2= Rпг·б= -Rлг·а+ Fм·(а+k). (8.19)
3.Равнодействующие реакции в опорах определяются геометрической суммой реакций в опорах в вертикальной и горизонтальной плоскостях:
- в левой опоре: Rл=√(Rлв)2+(Rлг)2 ; (8.20)
- в правой опоре: Rп=√(Rпв)2+(Rпг)2 ; (8.21)
- осевая реакция в левой опоре А=F0. (8.22)
4.Равнодействующий изгибающий момент в сечении 2-2 определяется
тоже геометрической суммой моментов в вертикальной и горизонталь-
ной плоскостях:
Ми2=√(Ми2в)2+(Ми2г)2 *. (8.21)
*Подставляется максимальное значение Ми2в - по формуле (8.12).
5.Изгибающий момент в сечении 1-1 уже определен в (8.18) и равен
Ми1= Fм·k.
«Опасным» сечением вала с точки зрения прочности является сечение 2 – 2 – в нëм действует максимальный изгибающий момент и крутящий момент.
Найденные реакции в опорах будут использоваться при проведении проверочного расчета ранее выбранных подшипников. Изгибающие моменты в сечениях и крутящий момент от сечения 1 – 1 до 2 – 2 – при проверочном расчете валов на усталостную и статическую прочность.
б. Проверочный расчет валов на усталостную прочность
Рис.8.6.Графики изменения нап-ряжений: а – изгиба, б - кручения
|
σи τкр τа
σа τm
σа t,c t,c
На практике установлено, что основным видом нарушения целостности валов является усталостное разрушение. Статическое разрушение происходит редко.
Установлено, что при вращении вала нап-
ряжения изгиба в различных точках попе-
речного сечения изменяются ся по сим-
метричному циклу, а напряжения круче-
ния – по пульсационному циклу, т.е. -
постоянные составляющие цикла напря- жений:
- изгиба σm = 0, (8.22)
- напряжений кручения – τm = τa = 0,5·τкр = Mкр/(0,4·d3)*. (8.23)
Переменные составляющие циклов напряжений:
- изгиба σа = σи = Ми/(0,1·d3)*, (8.24)
- кручения τкр = Mкр/(0,2·d3)*. (8.25)
*Моменты сопротивления без учета ослабления сечения наличием шпо-
ночного паза или отверстия.
Для усталостного расчета необходимо выбрать опасные сечения вала по
максимальным значениям изгибающих моментам, крутящего момента и наличии концентраторов напряжений (шпоночных пазов, отверстий, резьбы, галтелей сопряжения торцовых и цилиндрических поверхностей, канавок, предусмотренных конструкцией вала). Как правило, расчет выполняется в нескольких сечениях. Величины крутящего, изгибающего момента и диаметра вала в сечениях считаются уже рассчитанными.
При совместном действии напряжений кручения и изгиба коэффициент запаса усталостной прочности определяется по формуле:
nσ· nτ
n = ≥ [n] ≈ 1,5, (8.26)
√ nσ2 + nτ2
σ-1
где nσ = – коэффициент запаса усталостной прочности
kσ
σа + ψσ·σm только по изгибу; (8.27)
εм·εп
τ-1
nτ = – коэффициент запаса усталостной прочности
kτ
τа + ψτ·τm только по кручению; (8.28)
εм·εп
ψσ и ψτ – коэффициенты, корректирующие влияние постоянной состав-
ляющей цикла напряжений на усталостную прочность и зави-
сящие от механических характеристик материала вала (для
конструкционных низкоуглеродистых сталей ψσ = 0,05 и ψτ =
0, среднеуглеродистых сталей - ψσ = 0,10 и ψτ = 0,05, легирован-
ных сталей ψσ = 0,15 и ψτ = 0,10);
σ-1 и τ-1 – пределы усталостной прочности материала вала по напряжени-
ям изгиба и кручения (σ-1 ≈ (0,4…0,5) σв и τ-1 ≈ (0,2…0,3) σв));
εм и εп – коэффициенты соответственно масштабного фактора и фактора
качества поверхности расчетного сечения;
kσ и kτ – эффективные коэффициенты концентрации напряжений при из-
гибе и кручении в зависимости от концентратора напряжений
(и его параметра – табл.8.1).
8.1. Значения коэффициентов Кσ и Кτ
| Фактор концентрации напряжений | Кσ | Кτ | ||||||||||
| При σв, МПа или н/мм2 (:10кг/мм2; ·10 кг/cм2) | ||||||||||||
| ≤700 | ≈850 | ≥950 | ≤700 | ≈850 | ≥950 | |||||||
 Галтель:D/d = 1,25…2,0
       r/d: 0,02;
 0,06;
      0,10. d
D
r
|
2,50 1,85 1,60 |
3,00 1,93 1,62 |
3,50 2,00 1,64 |
1,80 1,40 1,25 |
1,90 1,47 1,30 |
2,10 1,53 1,35 | ||||||
| Канавка: r/d t/r: 1
 Сейчас читают про:
  8208 8059 | ||||||||||||
t
2
3
