Контрольные вопросы. Глава 5. Цифровые фильтры 1-го и 2-го порядков. Нерекурсивный фильтр 1-го порядка

Контрольные вопросы

1. Что такое микросхемы с "жесткой" и гибкой логикой? В чем преимущества и недостатки их с точки зрения применения в цифровых фильтрах?

2. Какова особенность канонической формы структурной схемы цифрового фильтра по сравнению с прямой формой?

3. Изобразите возможные структурные формы цифрового биквадратного блока.

4. В каком виде представляется выражение для передаточной функции цифрового фильтра, выполненного по параллельной форме?

5. При каком условии БИХ-фильтр 2-го порядка может быть представлен в последовательной структуре?

6. Назовите преимущества и недостатки параллельной и последовательной структур цифрового фильтра.

Глава 5. ЦИФРОВЫЕ ФИЛЬТРЫ 1-го и 2-го ПОРЯДКОВ

5.1. Нерекурсивный фильтр 1-го порядка

Передаточную функцию нерекурсивного фильтра 1-го порядка соста­вим из общего выражения (3.17), приняв a_k = 0 при 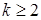 и b_k = 0 при :

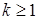                           .                            ( 5.1 )

При выбранных значениях коэффициентов a ₀ и   a ₁ из (3.20) получим разностное уравнение этого фильтра в виде:

                       y (n) = a ₀ x (n) + a ₁ x (n - 1).                                (5.2)

 Структурная схема фильтра, составленная на основе (5.2), показана на рис. 5.1,а. Для анализа удобнее несколько видоизменить уравнения (5.1) и (5.2), а также структурную схему фильтра.

 

 

Рис. 5.1.

Структурные схемы нерекурсивного фильтра 1-го порядка:

а) по уравнению (5.2), б) по уравнению (5.4).

 

Представим эти уравнения в виде:

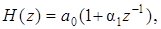                                                                (5.3)

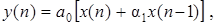                                                               (5.4)

где a₁ = a ₁/ a ₀.

Уравнениям (5.3) и (5.4) соответствует немного другая структурная схе­ма фильтра (рис. 5.1,б), из которой видно, что блок умно­жения входной последовательности x (п)на коэффициент а ₀ выполняет масштабирующие функции и не оказывает каче­ственного влияния на характеристики фильтра. Поэтому после того, как определен коэффициент a₁ = a ₁/ a ₀, этот блок может быть изъят из состава фильтра и отнесен к предшест­вующим или последующим каскадам общей структуры, в со­ставе которой находится рассматриваемый фильтр. Именно такое условие принимается в последующем анализе, а урав­нение (5.3) записывается в виде:

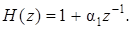                                                                 (5.5)

Предварительные cведения об АЧХ этого фильтра могут быть получены с помощью нуль-полюсной диаграммы. Представим (5.5) так:

                                                                           (5.6)

откуда следует, что функция (5.6) имеет один нуль z ₀ = - a₁ и один полюс в начале координат z _П= 0. Нуль-полюсная диаграмма и примерный вид АЧХ фильтра для случая a₁>0 показаны на рис. 5.2.

 

 

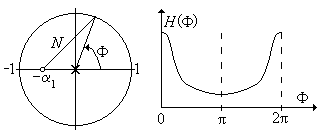
Рис. 5.2.

Нуль-полюсная диаграмма и АЧХ при a₁>0.

 

Рабочим диапазоном частот ЦФ является интервал Найквиста, в цифровых частотах это диапазон 0 ¸ p.  Очевидно, что принятое условие a₁ >0 соответствует фильтру нижних частот. Легко показать, что при a₁ < 0 нерекурсивный фильтр 1-го порядка является цифровым фильтром верхних частот.

Составим выражение для комплексного коэффициента передачи фильтра. Примем, как обычно, в (5.5) переменную z = exp(j F):

                                                                 (5.7)

и представим в (5.7) экспоненту от комплексного аргумента в тригономет­рической форме

                        H (j F) = 1 + a₁cosF - j a₁sinF.                               (5.8)

АЧХ фильтра определяем как модуль

                                                                 (5.9)

Уравнение фазочастотной характеристики (ФЧХ) фильтра составляем в соответствии с общим определением ФЧХ:

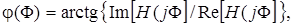                                          (5.10)

откуда

                                    

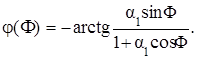
Ha рис. 5.3 показаны графики АЧХ и ФЧХ нерекурсивного фильтра 1-го порядка для различных коэффициентов a₁. Как и следовало ожидать, при a₁ = 1 (т.е. при a₁ >0) АЧХ соответствует фильтру нижних частот, при a₁ < 0 фильтр имеет бόльший коэффициент передачи в области верхних частот. Обратим внимание, что при a = ±1 ФЧХ абсолютно линейная. Линейность фазочастотной характеристики филь­тра необходима при обработке сигналов, у которых информационным параметром является фаза.

 

Рис. 5.3.

АЧХ и ФЧХ при различных значениях a₁.

 

Дискретная импульсная характеристика (ДИХ) фильтра определяется последовательностью коэффициентов передаточной функции H (z), представленной в виде полинома по степеням z ^{- k}. Это заключение непосредственно вытекает из определения функции H (z) (3.12):

                    

В рассматриваемом случае из (5.5) следует:

                                         (5.11)

 

Рис. 5.4.

ДИХ при различных значениях a₁.

 

Для выбранных на рис. 5.3 значений коэффициентов a₁ изображения ДИХ имеют вид, показанный на рис. 5.4. (рис. 5.4а) отсчеты ДИХ симметричны, при a₁ = - 1 (рис. 5.4б) они антисимметричны относительно оси, проходящей через абсциссу n = 1/2. При a₁ = 0,5 ДИХ не является ни симметричной, ни антисимметричной. Выше было отмечено, что при a₁ = ±1 ФЧХ имеют линейную зависимость от частоты. Связь степени линейности ФЧХ с симметрией или антисимметрией ДИХ является важным свойством КИХ-фильтров, оно будет подробно рассмотрено в главе 7.

Переходную характеристику g (n) найдем с помощью разностного уравнения (5.4). Для этого заменим x (n) на испытательное воздействие в виде цифровой единичной функции u (n), которая определяется выражением (1.3). При отрицательных номерах отсчетов x (- n) = 0, поэтому переходная характеристика имеет следующие значения: g (0) = a ₀, g (n ³ 1) = a ₀(1 + a₁). Таким образом, процесс установления заканчивается на отсчете с номером n = 1 и занимает один такт дискретизации.