Нерекурсивный фильтр 2-го порядка

Вначале, используя (3.17) и (3.20), составим исходные записи для передаточной функции рассматриваемого здесь фильтра

 

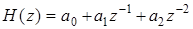                                                                (5.12)

и его разностного уравнения

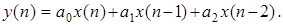                                             (5.13)

Преобразуем (5.12) и (5.13) с целью выделения коэффициен­та а ₀ как масштабирующего множителя и исключения его из состава этих уравнений. В результате получим:

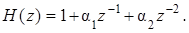                                                                 (5.14)

                                            (5.15)

где a₁ = a ₁/ a ₀, a₂ = a ₂/ a ₀.

Уравнениям (5.14) и (5.15) соответствует структурная схема фильтра, показанная на рис. 5.5. Выражение для комплексного коэффициента передачи фильтра получим из (5.14), положив z =exp(j F):

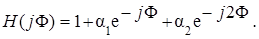                                           (5.16)

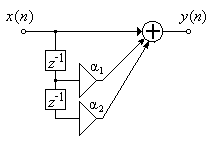
Рис. 5.5.

Структурная схема нерекурсивного фильтра 2-го порядка.

 

Представив экспоненты в тригонометрической форме, из (5.16) получим:

          (5.17)

где АЧХ H (F) и ФЧХ j(F) фильтра определяются так:

            (5.18)

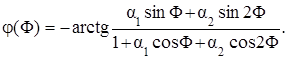                                    (5.19)

Найдем нули и полюсы передаточной функции (5.14). Для этого представим (5.14) в виде:

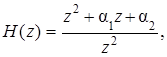                                                              (5.20)

откуда следует, что функция H (z) имеет двойной полюс в начале координат и два нуля:

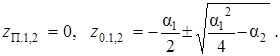                                        (5.21)

В зависимости от знака подкоренного выражения нули мо­гут быть действительными либо комплексно-сопряженными. Рассмотрим оба этих случая отдельно.

Действительные нули имеют место при a₁² - 4a₂ >0 и они могут располагаться только на действительной оси так, как это в качестве примера показано на рис. 5.6,а. На рис 5.6,бизображен примерный вид АЧХ, соответствующий выбраному расположению нулей.

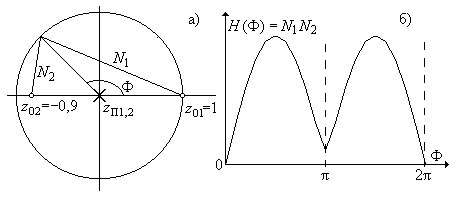
Рис. 5.6.

Нерекурсивный фильтр с действительными нулями: а) нуль-полюсная диаграмма, б) АЧХ.

 

Часто по известным (или выбранным) нулям необходимо составить выражение для передаточной функции фильтра. Связь между коэф­фициентами фильтра и нулями можно установить, представив числи­тель в (5.20) в виде:

            (5.22)

откуда следуют известные соотношения между корнями и коэффициентами квадратного трехчлена:

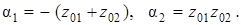                                                  (5.23)

В частности, размещению нулей на диаграмме рис. 5.6,асо­ответствует трехчлен

                                                

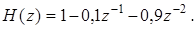
Для случая действительных нулей цифровой фильтр 2-го порядка можно представить в виде последовательной структуры. При этом (5.20) с использованием (5.22) записывается в виде

                                

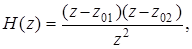
откуда следует

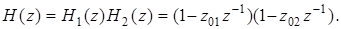                          (5.24)

 Уравнению (5.24) соответствует структурная схема цифрового фильтра, показанная на рис. 5.7.

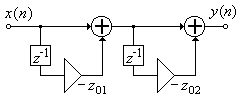
Рис. 5.7.

Последовательная структура нерекурсивного фильтра 2-го порядка.

 

Комплексно-сопряженные нули имеют место при a₁² - 4a₂ <0. Формулу для определения нулей запишем так:

         (5.25)

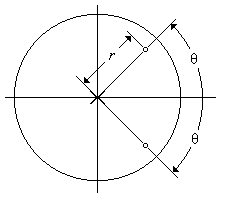
Рис. 5.8.

Нуль-полюсная диаграмма нерекурсивного фильтра 2-го порядка с комплексно-сопряженными нулями.

 

Из (5.25) следует, что комплексно-сопряженные нули распо­лагаются симметрично относительно действительной оси в верхней и нижней z -полуплоскостях (рис. 5.8). Определим связь между координатами нулей (r, q) и коэффициентами фильтра. Представив входящие в (5.23) выражения для нулей в тригонометрической форме (5.25)

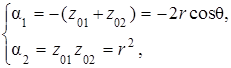                                                    (5.26)

получим уравнение нерекурсивного фильтра 2-го порядка с комплексно-сопряженными нулями:

                                                         (5.27)

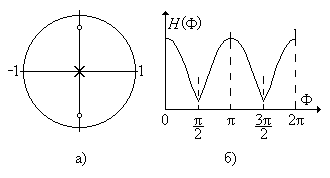
Рис. 5.9.

Нерекурсивный режекторный фильтр 2-го порядка: а) нуль-полюсная диаграмма, б) АЧХ.

 

Интересен частный случай, когда q = p/2, т.е. когда комплексно-сопряженные корни располагаются на мнимой оси (рис. 5.9,а). Поскольку при q = p/2 второй член в (5.27) равен нулю, структурная схема фильтра упрощается (рис. 5.10). Фильтр является режекторным со значительным (но не бесконечным) подавлением на частоте F = p/2 (рис. 5.9,б).

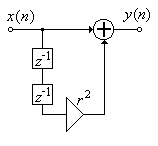
Рис. 5.10.

Структурная схема нерекурсивного режекторного фильтра 2-го порядка.

 

Для случая как комплексно-сопряженных, так и действительных нулей, ДИХ фильтра определяется коэффициентами передаточной функции (5.14) и, следовательно, содержит только три отсчета при n = 0, 1и 2. Если в фильтре на рис. 5.10 r = 1, то ДИХ фильтра симметрична (рис. 5.11), следовательно, ФЧХ абсолютно линейна.

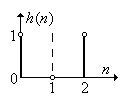
Рис. 5.11.

ДИХ режекторного фильтра 2-го порядка.

 

Переходную характеристику g (n) так же, как и для КИХ-фильтра 1-го порядка, определим с помощью разностного уравнения (5.15). Повторяя те же рассуждения, установим, что процесс установления занимает два такта дискретизации, а   g (n) имеет три отсчета: g (0) = 1, g (1) = 1 + a₁, g (n ³ 2) = 1+ a₁ + a₂.

При расчете КИХ-фильтров линейная координата одного или нескольких нулей иногда оказывается больше единицы. Такие нули, как правило, вводятся внутрь окружности единичного радиуса. Эта процедура сопровождается некоторыми особенностями, которые мы рассмотрим вначале на примере КИХ-фильтра 2-го порядка с комплексно-сопряженными нулями. Передаточную функцию фильтра запишем в виде:

  H (z) = 1 - 2 r ₀cosF₀ z ^-1 + r ₀² z ^-2 = 1 + a₁ z ^-1+ a₂ z ^-2.       (5.28)

Пусть линейная координата полюсов этого фильтра r ₀>1. Такой фильтр назовем исходным. ДИХ исходного фильтра определяется коэффициентами H (z) и содержит три отсчета:

                              h (0), h (1), h (2) ® 1, a₁, a₂.                           (5.29)

Фильтр с нулями, пересчитанными внутрь окружности единичного радиуса, будем называть модифицированным. Пересчет осуществляется в соответствии с равенством: r ₀' = 1/ r ₀, где r ₀' - линейная координата полюсов модифицированного фильтра. Его передаточную функцию запишем в виде:

                           H '(z) = 1 + a₁' z ^-1+ a₂' z ^-2.                   (5.30)

Коэффициенты передаточной функции модифицированного фильтра равны:

   

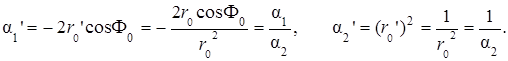
Введя полученные выражения для a₁'  и a₂' в (5.30), запишем выражение для передаточной функции модифицированного КИХ-фильтра в таком виде:

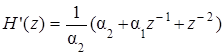                         .                           (5.31)

Множитель 1/a₂ играет роль масштабирующего коэффициента, который в нашем рассмотрении не имеет значения. Поэтому перепишем (5.30) так:

                            H '(z) = a₂ + a₁ z ^-1 +   z ^-2.                     (5.32)

Запишем отсчеты ДИХ модифицированного КИХ-фильтра:

                              h '(0), h '(1), h '(2) ® a₂, a₁, 1.                              (5.33)

 Сравнение показывает, что ДИХ исходного и модифицированного фильтров отличаются между собой. Проведем сравнение АЧХ фильтров.

Подставив в (5.28) и (5.32) z = exp(j F), запишем выражения для комплексного коэффициента передачи:

*  исходного фильтра:

         

*  модифицированного фильтра:

           

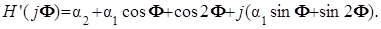
Теперь можно записать формулы для АЧХ фильтров. Чтобы не загромождать формулы знаком радикала, представим выражения для квадрата АЧХ:

*  исходного фильтра:

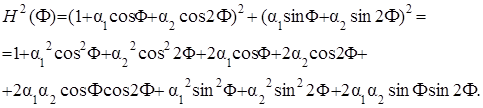     (5.34)

*  модифицированного фильтра:

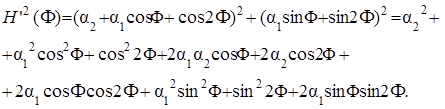             (5.35)

Выполнив преобразования в (5.34) и (5.35), получим:

   

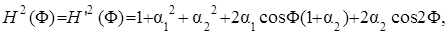
что говорит об идентичности АЧХ исходного и модифицированного фильтров.

Известно, что частотная характеристика любого линейного фильтра определяется спектром его импульсной характеристики. В нашем случае ДИХ двух ЦФ различны, а их АЧХ идентичны. Это, казалось бы, противоречие требует объяснения.

Сопоставляя (5.29) и (5.33), обнаруживаем, что по сравнению с (5.29) отсчеты h '(0) и h '(2) в (5.33) поменялись местами. Другими словами, ДИХ исходного и модифицированного фильтров зеркально симметричны. Это свойство ДИХ является ключом для разрешения отмеченного противоречия. Оно разъясняется в курсе "Радиотехнические цепи и сигналы", где показано, что два колебания u ₁(t) и u ₂(t) конечной длительности T _C, обладающие свойством зеркальной симметрии (рис. 5.12), имеют одинаковые амплитудные спектры. Такое свойство импульсных характеристик используется для создания так называемых оптимальных согласованных фильтров, обеспечивающих на выходе наибольшее отношение сигнал/шум. Фазовые спектры зеркально симметричных колебаний u ₁(t) и u ₂(t) отличаются между собой.

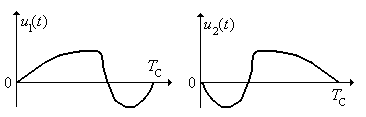
Рис. 5.12.

Колебания с зеркальной симметрией.

 

При модификации фильтра путем пересчета r ₀ в r ₀' = 1/ r ₀  внутрь окружности единичного радиуса перемещались оба комплексно-сопряженных нуля. Если в фильтре 2-го порядка оба нуля действительные и оба располагаются вне окружности единичного радиуса, то перемещать внутрь окружности можно либо оба нуля, либо только один. В первом случае ДИХ исходного и модифицированного фильтров будут зеркально симметричны, во втором случае зеркальная симметрия будет иметь место только у ДИХ звена 1-го порядка, подвергнутого модификации. В то же время АЧХ каждого звена 1-го порядка и фильтра 2-го порядка, состоящего из этих звеньев, остается без изменения, подвергаются ли модификации оба нуля или один из них.