Характеристики цифрового биквадратного блока

Отдельное рассмотрение нерекурсивных и рекурсивных ЦФ 2-го порядка позволяет определить характеристики цифрового биквадратного блока с передаточной функцией

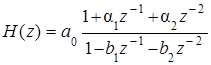                             .                                     (5.66)

Запишем (5.66) в виде

       .       

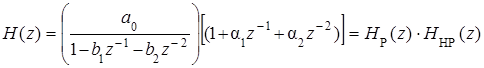Такая запись дает возможность представить цифровой блок как каскадное включение рекурсивного и нерекурсивного фильтров, как это показано на рис. 5.25. На этом рисунке x (n) – входная цифровая последовательность биквадратного блока, w (n) – цифровая последовательность на выходе рекурсивного фильтра, y (n) – выходная цифровая последовательность нерекурсивного фильтра, она же – выходная цифровая последовательность всего биквадратного блока.

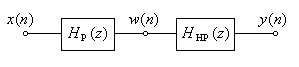
Рис. 5.25.

Каскадное включение рекурсивного и нерекурсивного фильтров.

 

АЧХ цифрового блока определяется произведением АЧХ рекурсивного и нерекурсивного фильтров:

  

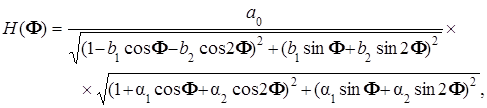
а фазочастотная характеристика блока определяется суммой фазовых сдвигов рекурсивной и нерекурсивной частей блока:

.

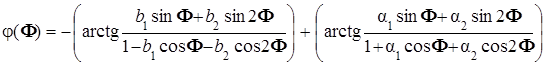Найдем выражение для ДИХ h (n) цифрового биквадратного блока. Ее можно определить несколькими способами.

Во-первых, ДИХ является обратным z -преобразова­нием передаточной функции блока (5.66), и ее (ДИХ) можно найти, используя выражение (3.10) в гл. 3.

Во-вторых, ДИХ блока можно найти, если решить разностное уравнение его нерекурсивной части: 

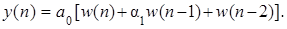                                                    (5.67)

Мы воспользуемся именно этим способом. Но вначале, с целью получения более расширенного представления о свойствах ЦФ, определим разностное уравнение нерекурсивного фильтра, не обращаясь к его готовой записи (5.67).

По определению, ДИХ   h (n) всего биквадратного блока является его выходной последовательностью y (n), если на вход  блока подать единичный отсчет d(n), т.е. установить x (n) = d(n).

С другой стороны, при каскадной форме структуры блока его выходную последовательность y (n) можно представить как результат дискретной свертки ДИХ нерекурсивной части h _НР(n) с последовательностью w (n), действующей на входе нерекурсивной части:

                                       .

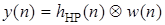Последовательность w (n) – это выходная последовательность рекурсивной части биквадратного блока. При подаче на вход блока единичного отсчета последовательность w (n) представляет собой ДИХ рекурсивной части h _Р(n).

Таким образом, ДИХ биквадратного блока h (n) является результатом свертки дискретных импульсных характеристик рекурсивной и нерекурсивной частей:

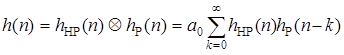                .                      (5.68)

ДИХ h _НР(n), входящая в (5.68), содержит всего три отсчета, поэтому удобнее (5.68) записать в развернутом виде:

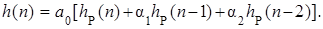                                                (5.69)

Сравнивая (5.67) и (5.69), убеждаемся, что применительно к КИХ-фильтру процедура свертки по сути является решением разностного уравнения этого фильтра.

Введем в (5.69) общее выражение (5.52) для ДИХ рекурсивного фильтра 2-го порядка. Напомним, что выражение (5.52) составлялось в предположении, что z _П1 ≠ z _П2. Константу   a,входящую в выражение (5.52), включим в a ₀. В результате получим:

  (5.70)

Выражение (5.70) можно использовать непосредственно в случае, когда полюсы z _П.1,2 передаточной функции (5.44) действительные. Если полюсы комплексно-сопряженные, то в выражение (5.69) следует ввести выражение (5.63), и тогда:

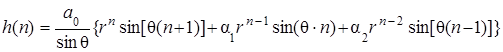,  (5.71)

где r и ±q –  полярные координаты полюсов.

Формулы (5.70) и (5.71) в том виде, как они представлены, могут использоваться только для значений   n ≥2.  Действительно, ДИХ любого ЦФ не существует в области отрицательных значений n. Обращаясь к (5.69), устанавливаем, что h _Р(n – 1) = 0 при n = 0 и h _Р(n – 2) = 0 при n = 0 и n = 1. Отмеченное обстоятельство не приводит к каким-либо существенным осложнениям в расчете ДИХ цифрового блока. Поскольку первый отсчет (при n =0) ДИХ любого БИХ-фильтра всегда равен h (0) = a ₀, то дополнительное определение требуется для единственного отсчета ДИХ с номером n =1. Его найдем из (5.70):

    

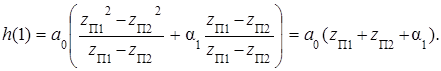
В соответствии с (5.47): z _П1 + z _П2 = b ₁, поэтому последнее выражение перепишем в виде:

                               h (1) = a ₀(b ₁ + a₁).

Последним выражением можно пользоваться как при действительных, так и при комплексно-сопряженных полюсах. В последнем случае, как это показано в (5.61), b ₁ = 2 r cosq, и тогда

                        h (1) = a ₀(2 r cosq+ a₁).                                           (5.72)

В качестве примера рассмотрим цифровой биквадратный блок с передаточной функцией

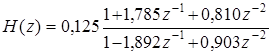               .                          (5.73)

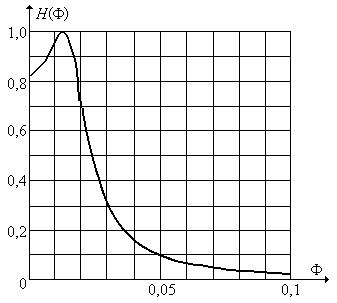
Рис. 5.26.

АЧХ биквадратного блока с передаточной функцией (5.73).

 

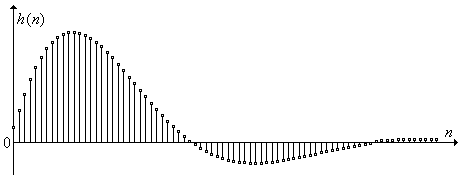
Рис. 5.27.

ДИХ биквадратного блока с передаточной функцией (5.73).

 

АЧХ этого блока показана на рис. 5.26, а график ДИХ – на рис. 5.27. Необходимые для расчета ДИХ числовые значения величин, входящих в (5.71) и (5.72), равны:

a₀ = 0,125; a₁ = 1,785; a₂ = 0,810; r = 0,95; q = p/34.