2021-11-13
199
Способы описания цифровых фильтров
Задача 7. ЦФ задан передаточной функцией:
.
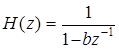Определите реакцию ЦФ на входное воздействие x (n) = (– 1) n.
Решение. Определим выходную последовательность y (n), используя обратное z -преобразование от Y (z). Функцию Y (z) найдем из выражения:
Y (z) = X (z)· H (z), (1)
где
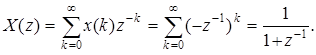(2)
Подставив (2) в (1), получим:
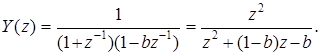(3)
Обратное z -преобразование выражения (3) выполним по методу, описанному в Приложении 3:
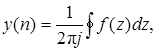
где
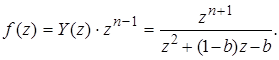
Представим f (z) в виде f (z) = f 1(z)/ f 2(z) и найдем y (n) с помощью вычетов:
где z 1 и z 2 – корни знаменателя в f (z): z 1 = – 1, z 2 = b.
Выполнив необходимые подстановки и преобразования, получим:
.
В качестве примера на рис. П1.7 показан график последовательности y (n), построенный при b = 0,9. Отметим, что | y (n)| → 0,526 при n → ∞.
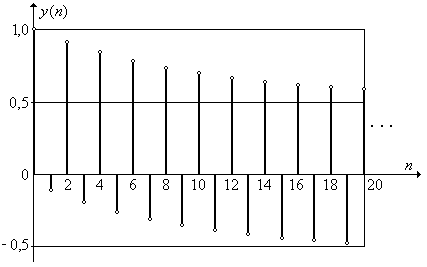
Рис. П1.7. Реакция ЦФ.
Задача 8. ЦФ задан передаточной функцией:
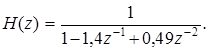
Определите реакцию ЦФ на действие сигнала x (n), состоящего из двух единичных отсчетов, разделенных одним интервалом дискретизации T (рис. П1.8).
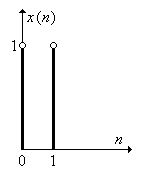
Рис. П1.8. Входное воздействие.
Решение. Заданный ЦФ является БИХ-фильтром 2-го порядка с двумя кратными полюсами z П1 = z П2 = 0,7. ДИХ такого фильтра определена в подразделе 5.4:
h (n) = z П n ×(n + 1). (1)
Если на входе действует один единичный отсчет, то откликом фильтра является ДИХ. Поскольку на входе действуют два единичных отсчета, сдвинутых относительно друг друга на интервал T, то выходной эффект будет определяться суммой двух ДИХ, одна из которых запаздывает на такой же интервал T:
y (n) = h (n) + h (n - 1). (2)
Подставив (1) в (2), получим следующее выражение для выходного эффекта фильтра:
y (n) = z п n (n + 1) + z п n -1× n = z п n -1[(z п + 1) n + z п].
График y (n) при z п = 0,7 показан на рис. П1.9.
Рис. П1.9. Выходное воздействие.
Задача 9. Известна переходная характеристика ЦФ:
g (n) = 1 – bn + 1.
Определите передаточную функцию ЦФ.
Решение. Определим H (z) из выражения:
H (z) = G (z)/ X (z), (1)
где G (z) и X (z) – z -преобразования, соответственно, переходной характеристики и входного воздействия.
Испытательным воздействием при снятии переходной характеристики ЦФ является цифровая единичная функция
x (n) = u (n) = 1 при n ≥ 0.
Ее z -преобразование определяется выражением:
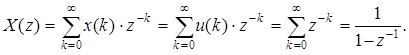(2)
Определим z -преобразование переходной характеристики:
После ряда преобразований получим:
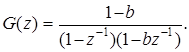(3)
Подставив (2) и (3) в (1), получим:
.
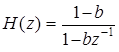Задача 10. ЦФ нижних частот задан передаточной функцией:
H (z) = 1 + z – 1.
Определите реакцию ЦФ на входное воздействие x (n) = 0,9 n.
Решение. При решении некоторых задач целесообразно представлять ЦФ не как частотно-избирательное устройство, а как функциональный блок, выполняющий те или иные математические операции. В данном случае разностное уравнение ЦФ y (n) = x (n) + x (n – 1) показывает, что отсчеты выходной последовательности y (n) определяются суммой текущего и предыдущего отсчетов входной последовательности, т.е.
y (n) = 0,9 n + 0,9 n – 1. (1)
Преобразуя (1), получим:
y (n) = 0,9 n (1 + 0,9 – 1) = 0,9 n ·2,11 ≈ 2 x (n).
Такой результат вполне очевиден. Действительно, во входной последовательности x (n) = 0,9 n. При этом любые два соседних отсчета мало отличаются по уровню, что и приводит к увеличению отсчетов y (n) примерно в два раза по сравнению с x (n).
Задача 11. ЦФ верхних частот задан передаточной функцией:
H (z) = 1 – z – 1.
Определите выходной эффект при действии на входе последовательностей:
а) x (n) = n, б) x (n) = n 2,
где n – целое число и n ≥ 0.
Решение. В данной задаче имеет смысл рассматривать ЦФ как вычислительное устройство, которое в соответствии с разностным уравнением
y (n) = x (n) – x (n – 1) (1)
определяет разность текущего отсчета x (n) с предшествующим x (n – 1), т.е. выполняет роль цифрового дифференциатора. В случае а), используя (1), получим:
y (n) = n – (n – 1) = 1.
Рассмотрим геометрическую интерпретацию результатов. Функция x (n) = n представляет собой наклонную прямую. Производная этой функции, т.е. y (n) является постоянной величиной со значением 1.
Для случая б) получим, с использованием (1):
y (n) = n 2 – (n – 1)2. (2)
При n = 0 входной отсчет x (n) = 0, следовательно, при нулевых начальных условиях, и выходной отсчет y (n) должен равняться нулю. В связи с этим, определять y (n) по выражению (2) следует, начиная с n = 1:
y (n) = 2 n – 1, n ≥ 1. (3)
Полученный результат отличается от производной функции x (n) = n 2,
которая равняется 2 n. Отличие можно объяснить тем, что разностное уравнение, описывающее цифровой фильтр, является уравнением в конечных разностях, в отличие от дифференциального уравнения. Найдем погрешность цифрового дифференциатора, определяя ее в виде:
Подставляя сюда y (n) из (3), получим:
d = 1/2 n,
откуда следует, что погрешность уменьшается с ростом n.
Задача 12. ЦФ задан передаточной функцией:
. (1)
С использованием выражения (1) составлено разностное уравнение:
y (n) = 1,4[ x (n) + 0,6 x (n - 1) - 0,4 x (n - 2) - 0,8 y (n - 1) + 0,7 y (n - 2)].
Однако эта запись содержит ошибки. Найдите их.
Решение. Правильное выражение имеет вид:
y (n) = 1,4[ x (n) + 0,6 x (n - 1) - 0,4 x (n - 2)] + 0,8 y (n - 1) - 0,7 y (n - 2)].
Задача 13. Дано разностное уравнение ЦФ нижних частот:
y (n) = 0,1 x (n) + 0,15 x (n – 1) + 0,05 x (n – 2) + y (n – 1) – 0,25 y (n – 2).
Определите коэффициент передачи ЦФ на нулевой частоте.
Решение. Выполнив z -преобразование разностного уравнения, составим выражение для передаточной функции:
.
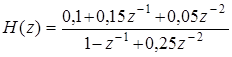Для определения комплексного коэффициента передачи надо положить z = exp(j F). На нулевой частоте F = 0, соответственно z = 1. Подставив это значение в выражение для H (z), получим:
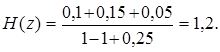
З адача 14. ЦФ задан разностным уравнением:
y (n) = x (n) + 1,5 x (n – 1) + 0,5 x (n – 2) + 1,13 y (n – 1) – 0,64 y (n – 2). (1)
Используя только разностное уравнение (не прибегая к составлению передаточной функции или выражению для АЧХ), рассчитайте коэффициент передачи ЦФ для постоянной составляющей.
Решение. Решение задачи основано на том, что в установившемся режиме коэффициент передачи постоянной составляющей численно равен постоянному уровню выходных отсчетов ЦФ при действии на входе единичной функции u (n). Напомним, что u (n) = 1 при n ≥ 0. Для рассматриваемой задачи в установившемся режиме
(2)
Подставляя (2) в (1), получим:
y (n) = 1 + 1,5 + 0,5 + 1,13 y (n) – 0,64 y (n),
откуда
Задача 15. Рассматривается БИХ-фильтр 1-го порядка, ДИХ которого h (n) = bn. Определите отклик этого фильтра на входную последовательность x (n) = bn.
Решение. Известно, что ЦФ, имеющий ДИХ h (n) = bn, описывается передаточной функцией:
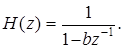
Z -преобразование X (z)входного воздействия x (n) = h (n) = bn описывается таким же выражением. Следовательно, z -форма выходной последовательности y (n) равна:
Y (z) = X (z)× H (z) = [ H (z)]2 = 1/(1 - bz -1)2
В Приложении 3 для аналогичной задачи показано, как с помощью вычетов найти обратное z -преобразование от Y (z), т.е. выходной отклик y (n). Этот отклик определяется выражением:
y (n) = (n + 1) bn.
Задача 16. На рис. П1.10 изображены нуль-полюсная диаграмма (НПД) и АЧХ ЦФ. НПД содержит два нуля с координатами – 1,0 и +1,0 и два полюса в начале координат (в центре круга). Определите, увеличится или уменьшится значение Hm, если полюсы из центра круга сместить в точки z П 1,2 = ± 0,5.
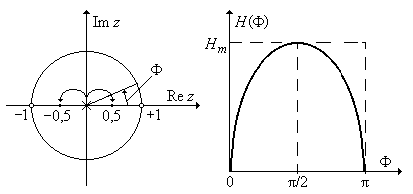
Рис. П1.10. НПД и АЧХ цифрового фильтра.
Решение. Метод определения АЧХ с использованием НПД рассматривался в главе 3. Расчетная формула имеет вид:
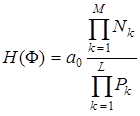, (1)
где a 0 – постоянный коэффициент, Nk и Pk – расстояние от точки на окружности с угловой координатой F, соответственно, до k -того нуля или до k -того полюса.
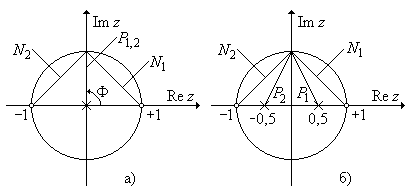
Рис. П1.11. Определение расстояний до особых точек: а) до смещения полюсов; б) после смещения полюсов.
Используем эту формулу в нашей задаче. Положим a 0 = 1. Нетрудно установить, что максимальное значение АЧХ, равное Hm, в данной задаче реализуется когда F = p/2. При исходном расположении нулей и полюсов расстояние до каждого нуля равно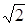 
, а до каждого полюса 1. В этом случае расчет по (1) дает (см. также рис. П1.11а):
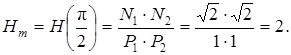
После смещения полюсов НПД выглядит так, как показано на рис. П1.11б. Расстояния до нулей не изменились, а расстояния до полюсов приняли значение:
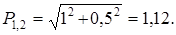
Теперь значение Hm равно:
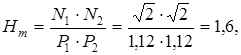
т.е. стало меньше прежнего.
Задача 17. Определите, чему равен коэффициент передачи ЦФ на нулевой частоте H (0), если НПД имеет вид, приведенный на рис. П1.12.
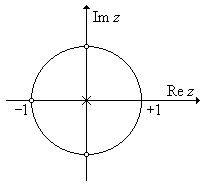
Рис. П1.12. Заданная НПД фильтра.
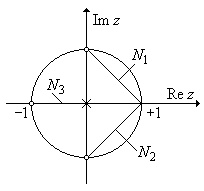
Рис. П1.13. Построения на НПД.
Решение. На нуль-полюсной диаграмме проведем отрезки (рис. П1.13), соединяющие точку на окружности, угловая координата которой F = 0, с нулями передаточной функции. Длины этих отрезков представляют собой расстояния Nk. Для определения значения H (0) воспользуемся выражением (1) из задачи 9.16 и положим a 0 = 1. В результате получим:
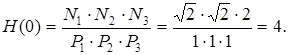
Задача 18. ЦФ задан передаточной функцией:
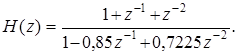
Изобразите нуль-полюсную диаграмму (НПД) и примерный вид графика АЧХ.
Решение. Для отыскания особых точек передаточной функции запишем ее выражение с положительными степенями z:
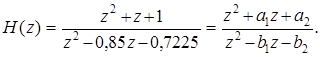
Дискриминанты выражений в числителе и знаменателе – отрицательные. Таким образом, как нули, так и полюсы H (z) – комплексно-сопряженные. Выразим координаты нулей и полюсов в полярных координатах:
– линейная координата нулей: R 0 =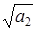 
=1;
– угловая координата нулей: F0 = arccos(– a 1/2 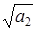) = ±1200 = ±2p/3.
– линейная координата полюсов: R П =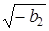 
= 0,85;
– угловая координата полюсов: FП = arccos(b 1/2 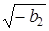) = ±600 = ±p/3.
НПД и примерный вид АЧХ показаны на рис. П1.14.
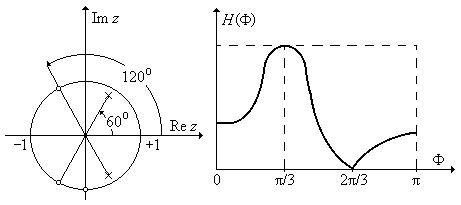
Рис. П1.14. НПД и примерный вид АЧХ ЦФ.
Задача 19. ЦФ задан передаточной функцией: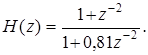 
Изобразите примерный вид графика АЧХ этого ЦФ.
Решение. Найдя нули и полюсы передаточной функции: z 0 1,2 = = exp(± j p/2); z П 1,2 = 0,9exp(± j p/2), построим нуль-полюсную диаграмму (рис. П1.15).
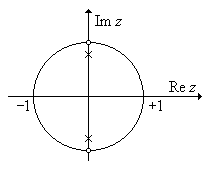
Рис. П1.15. НПД фильтра в задаче 19.
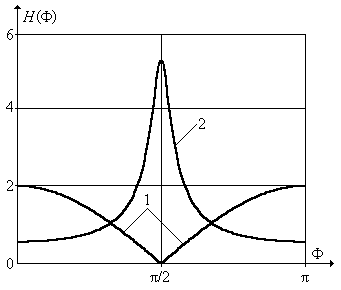
Рис. П1.16. АЧХ рекурсивной и нерекурсивной частей фильтра.
На рис. П1.16 изображены АЧХ – отдельно для нерекурсивной (кривая 1) и рекурсивной (кривая 2) частей передаточной функции фильтра. Перемножение этих АЧХ дает результирующую режекторную характеристику (рис. П1.17). Отметим, что режекторную характеристику можно сформировать, используя только нерекурсивную часть, как это видно из рис. П1.16. Однако включение рекурсивной части способствует резкому сужению полосы режекции, которая тем ýже, чем ближе расположены полюсы рекурсивной части к окружности единичного радиуса.
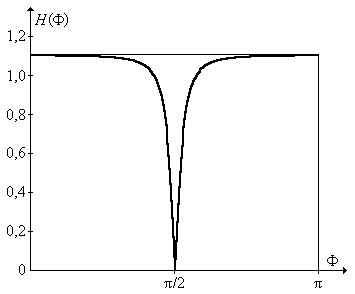
Рис. П1.17. Результирующая АЧХ фильтра.
Задача 20. К какому типу фильтров (ФНЧ, ФВЧ, ПФ или РФ) относится ЦФ с передаточной функцией:
?
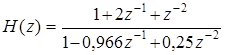Решение. Построим обычным образом нуль-полюсную диаграмму (рис. П1.18). Ее изучение позволяет сделать следующие выводы.
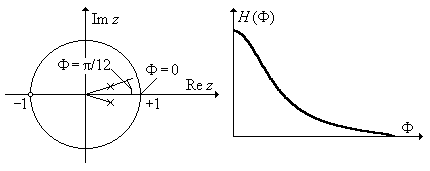
Рис. П1.18. НПД и АЧХ фильтра в задаче 20.
Во-первых, в области малых значений F, что соответствует области нижних частот, значения коэффициента передачи отличаются от нуля. Во-вторых, при значениях F, близких к p, что соответствует области верхних частот, коэффициент передачи уменьшается до нуля.
Из этого можно сделать вывод, что рассматриваемый фильтр – не ФВЧ и не РФ. Он может использоваться как ФНЧ или даже ПФ, если АЧХ имеет выраженный резонансный характер. Из нуль-полюсной диаграммы однако видно, что расстояния от окружности до полюсов при F = 0 и F = p/12 несущественно отличаются друг от друга. Следовательно, примерно одинаковы и значения АЧХ в области цифровых частот от F = 0 до F = p/12, а, значит, рассматриваемый ЦФ является фильтром нижних частот. Результаты проведенного качественного анализа подтверждаются рассчитанной АЧХ, приведенной на рис. П1.18.
Задача 21. Дана нуль-полюсная диаграмма КИХ-фильтра 1-го порядка (рис. П1.19). Выведите выражение для АЧХ, используя формулу (3.36) из главы 3.
Рис. П1.19. НПД фильтра в задаче 21.
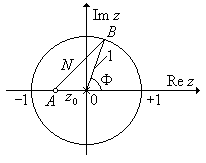
Рис. П1.20. Построения на НПД для определения АЧХ.
Решение. Применительно к КИХ-фильтру 1-го порядка формула (3.36) принимает вид: H (F) = N (F), где N (F) – расстояние от точки на окружности с угловой координатой F до точки расположения нуля z 0 (рис. П1.20). В треугольнике A 0 B выразим длину стороны AB = N через длины двух других сторон:
.
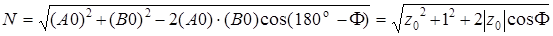В подкоренном выражении фигурируют длины, поэтому z 0 надо брать по модулю.
Подставляя в это выражение z 0 = a1, получим:
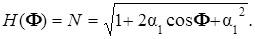
Это выражение совпадает с выражением для АЧХ, полученным из передаточной функции H (z) (формула (5.9) гл. 5).
Задача 22. Определите ДИХ цифрового КИХ-фильтра, если известна его переходная характеристика g (n) (рис. П1.21).
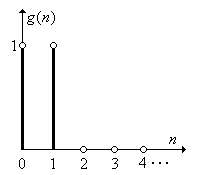
Рис. П1.21. Переходная характеристика фильтра в задаче 22.
Решение. Поскольку исследуемый ЦФ является КИХ-фильтром, то его ДИХ определяется коэффициентами передаточной функции, исходную запись для которой составим так:
H (z) = G (z)/ X (z), (1)
где G (z) - z -форма переходной характеристики:
(2)
а X (z) - z -форма входного испытательного воздействия, которым, для получении g (n), является цифровая единичная функция.
Так как цифровая единичная функция определяется в виде:
x (n) = 1, при n ³ 0 и x (n) = 0, при n < 0,
то для X (z) получаем выражение:
(3)
Подставив (2) и (3) в (1), получим:
H (z) = (1 + z -1)(1 - z -1) = 1 - z -2.
Следовательно h (n) будет иметь отсчеты: 1, 0, - 1. График ДИХ приведен на рис. П1.22.
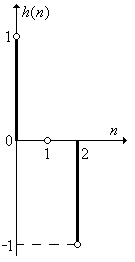
Рис. П1.22. График ДИХ в задаче 22.
Задача 23. ЦФ задан передаточной функцией:
H (z) = 1 + a1 z -1 + a2 z -2,
где a2 =1. Как влияет коэффициент a1 на фазочастотную характеристику этого ЦФ?
Решение. Для получения ответа на поставленный вопрос нет необходимости прибегать к помощи формулы (5.19) главы 5. Достаточно обратить внимание на то, что ДИХ рассматриваемого ЦФ имеет отсчеты 1, a1, 1, и, следовательно, является симметричной. Для КИХ-фильтра с симметричной КИХ, вне зависимости от значений отсчетов, ФЧХ всегда линейная.
Задача 24. Два цифровых КИХ-фильтра имеют различные передаточные функции:
ЦФ1: H 1(z) = 0,5(1 – 1,7 z – 1 + 0,72 z – 2);
ЦФ2: H 2(z) = 0,4(1 – 2,15 z – 1 + 1,125 z – 2),
однако их АЧХ совершенно одинаковы, как это показано на рис. П1.23, где совпадающие АЧХ обозначены H 1,2(F). Как это объяснить?
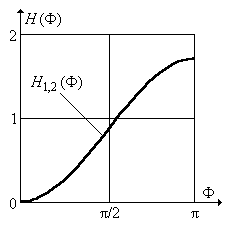
Рис. П1.23. Совпадающие АЧХ двух ЦФ.
Решение. Выразим передаточные функции через положительные степени z:
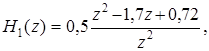
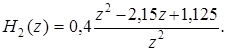
Найдем координаты нулей
ЦФ1: z 01-1 = 0,8; z 02-1 = 0,9.
ЦФ2: z 01-2 = 1,25; z 02-2 = 0,9.
Так как корни действительные, то передаточные функции можно представить в виде произведения множителей 1-го порядка:
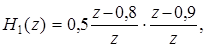(1)
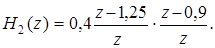(2)
Рассмотрим отдельный множитель, записав его в виде:
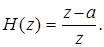
Пусть a < 1. Найдем особые точки: нуль z 0 = a и полюс z П = 0 и изобразим их на нуль-полюсной диаграмме (рис. П1.24).
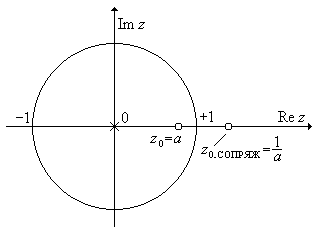
Рис. П1.24. Сопряженные нули передаточной функции в задаче 24.
Так как полюс находится в центре круга, то он не влияет на АЧХ. АЧХ зависит только от расположения нуля z 0 = a и определяется выражением:
Покажем, что такую же АЧХ будет иметь звено с передаточной функцией
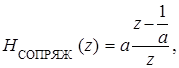(3)
у которой нуль является сопряженным с нулем z 0 = a:
z 0.СОПРЯЖ = 1/ z 0 = 1/ a.
Подставив в (3) z = exp(j F), найдем:
Рассмотрим первые множители в выражениях (1), (2). Исходя из изложенного, очевидно, что нули этих множителей являются сопряженными, следовательно, АЧХ H 1(F) и H 2(F) совпадают. Отметим, что ФЧХ j1(F) и j2(F) неидентичны.
Задача 25. Найти передаточную функцию режекторного КИХ-фильтра 2-го порядка. Цифровая частота абсолютной режекции FР = p/3. Во сколько раз отличаются коэффициенты передачи ЦФ на частотах, соответствующих концам интервала Найквиста?
Решение. Так как КИХ-фильтр должен обеспечивать абсолютную режекцию, т.е. нулевой коэффициент передачи, то нули должны располагаться на окружности единичного радиуса. При частоте режекции FР = = p/3 угловая координата нулей равна ±p/3. Передаточная функция имеет вид:
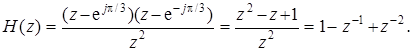
Нуль-полюсная диаграмма изображена на рис. П1.25. Оба полюса КИХ-фильтра расположены в центре круга единичного радиуса и не влияют на АЧХ. График АЧХ приведен на рис. П1.26. Найдем значения коэффициентов передачи H (0) и H (p) на концах интервала Найквиста. Для этого используем построения на рис. П1.25 и формулу (1) из задачи 16, полагая a 0 = 1. В результате получим: H (0) = (1·1) = 1, H (p) =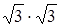 
= 3 и H (p)/ H (0) = 3.
Рис. П1.25. НПД фильтра в задаче 25.
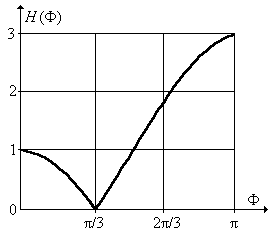
Рис. П1.26. АЧХ фильтра в задаче 25.
Задача 26. Рассчитайте ЦФ минимального порядка по заданной на рис. П1.27 АЧХ (требования по переходным зонам не оговариваются).
Рис. П1.27. АЧХ, заданная в задаче 26.
Решение. В качестве прототипа заданного ЦФ используем режекторный фильтр, рассмотренный в задаче 25.
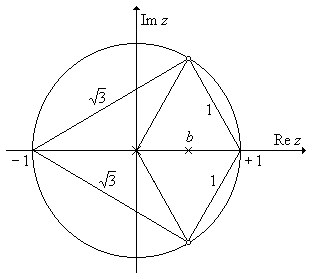
Рис. П1.28. НПД фильтра к задаче 26.
Для выравнивания значений H (0) и H (p) введем действительный полюс с координатой b. При этом нуль-полюсная диаграмма будет иметь вид, приведенный на рис. П1.28. Для отыскания значения b обратимся к формуле (1) из задачи 16, в которой положим a 0 = 1. Согласно этой формуле и рис. П1.28, можно записать: H (0) = (1·1)/(1 – b), H (p) = 
/(1 + b). Для обеспечения равенства H (0) = H (p) необходимо, чтобы b = 0,5. При таком значении b оказывается, что H (0) = H (p) = 2. Следовательно, масштабирующий множитель a 0 надо принять равным 0,5. Передаточная функция ЦФ примет вид:
.
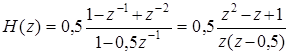Задача 27. Составьте выражения для передаточных функций ЦФ, структурные схемы которых показаны на рис. П1.29.
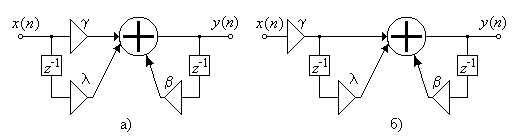
Рис. П1.29. Структурные схемы по вариантам а) и б) к задаче 27.
Решение. Вариант а)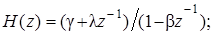 
вариант б)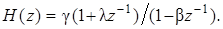 
Задача 28. Преобразуйте структуру ЦФ, показанную на рис. П1.30, в каноническую форму.
Рис. П1.30. Структурная схема ЦФ к задаче 28.
Решение. На рис. П1.30 приведена структура фильтра, состоящего из двух параллельно включенных фильтров 1-го порядка - нерекурсивного, с передаточной функцией H 1(z), и рекурсивного, с передаточной функцией H 2(z). Передаточная функция описывается выражением:
(1)
где a = 0,9 и b = 0,6.
Для преобразования структуры на рис. П1.30 в каноническую форму необходимо передаточную функцию ЦФ представить в виде дробно-рациональной функции. Делается это путем приведения правой части в (1) к общему знаменателю:
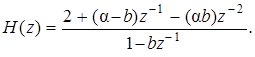
Полученной передаточной функции соответствует искомая структурная схема, приведенная на рис. П1.31.
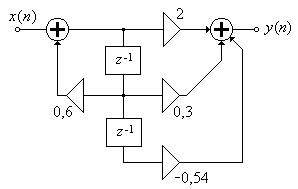
Рис. П1.31. Каноническая структура ЦФ.
ЦФ со структурами на рис. П1.30 и рис. П1.31 обладают абсолютно идентичными характеристиками (АЧХ, ДИХ и т.д.), однако реализация фильтра по структуре на рис. П1.31 нецелесообразна ввиду ее большей сложности.
Задача 29. Задана ДИХ ЦФ: h (n) = pn + qn. Составьте структурную схему ЦФ в канонической форме. Как изменится структура ЦФ, если принять p = q?
Решение.
Заданная ДИХ относится к двум БИХ-фильтрам 1-го порядка, включенным параллельно. Передаточная функция такого ЦФ имеет вид:
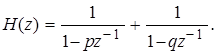(1)
Выполнив в (1) приведение к общему знаменателю, получим передаточную функцию однокаскадного ЦФ:
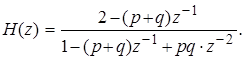(2)
Выражению (2) соответствует структурная схема, приведенная на рис. П1.32.
Рис. П1.32. Структурная схема ЦФ в задаче 29.
Если принять p = q = r, то (2) примет вид:
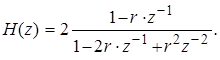(3)
Эта передаточная функция содержит два кратных полюса z П.1,2 = r, один из которых компенсируется единственным нулем с таким же значением r: z 0 = r. В результате передаточная функция (3) принимает вид:
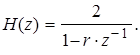(4)
В соответствии с (4) структурная схема ЦФ упрощается и принимает вид, показанный на рис. П1.33.
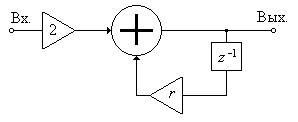
Рис. П1.33. Структурная схема ЦФ при p = q = r.
Задача 30. Можно ли упростить структурную схему ЦФ, приведенную на рис. П1.34?
Рис. П1.34. Заданная структурная схема к задаче 30.
Решение. Составим разностное уравнение по приведенной структурной схеме:
y (n) = x (n) – 0,25 x (n – 2) + 0,5 y (n – 1).
От разностного уравнения перейдем к передаточной функции:
.
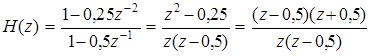Из выражения для H (z) следует, что нуль z 0 = 0,5 компенсирует полюс z П = 0,5, при этом передаточную функцию можно переписать в виде:
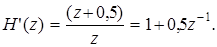
Передаточной функции H '(z) соответствует разностное уравнение:
y '(n) = x (n) + 0,5 x (n – 1)
и упрощенная структурная схема, показанная на рис. П1.35.
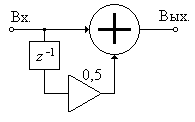
Рис. П1.35. Упрощенная структурная схема к задаче 30.
Задача 31. Два цифровых биквадратных блока были рассчитаны отдельно и затем объединены в двухкаскадный ЦФ. Оказалось, что полученная структура (рис. П1.36) может быть существенно упрощена. Сделайте это.
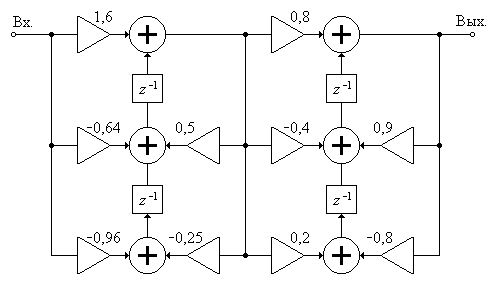
Рис. П1.36. Структура ЦФ, заданная в задаче 31.
Решение. Иногда в передаточной функции ЦФ обнаруживаются нули и полюсы, имеющие одинаковые координаты. В этом случае они взаимно компенсируются, что приводит к сокращению порядка ЦФ и, соответственно, к упрощению его структуры. Именно такое обстоятельство имеет место в поставленной задаче. Запишем передаточную функцию ЦФ, представленного на рис. П1.36:
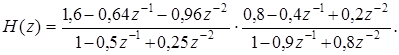
Преобразуем это выражение:
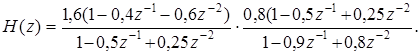
Из последней записи видно, что оба полюса первого каскада компенсируются нулями второго, и тогда передаточная функция принимает вид:
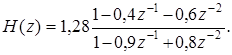
По последнему выражению составлена структурная схема ЦФ в канонической форме, которая приведена на рис. П1.37.
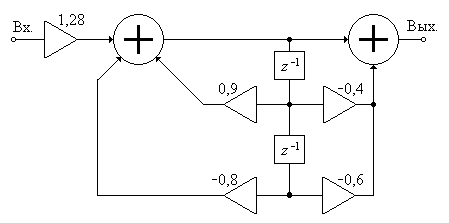
Рис. П1.37. Упрощенная структура к задаче 31.
Задача 32. Составьте структурные схемы в последовательной и параллельной формах для ЦФ с передаточной функцией:
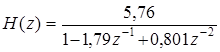. (1)
Решение. Передаточная функция в (1) содержит два кратных полюса z П.1,2 = = 0,895. Для составления последовательной структуры функцию (1) представим в виде:
,
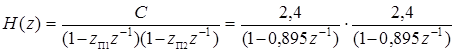откуда следует, что последовательная структура реализуется в виде двух идентичных каскадов – БИХ-фильтров 1-го порядка (рис. П1.38).
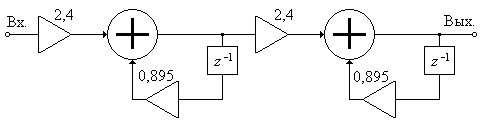
Рис. П1.38. Последовательная структура ЦФ к задаче 32.
Для реализации ЦФ в параллельной форме функцию (1) следует представить так:
,
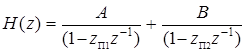где величины A и B могут быть вычислены, например, методом неопределенных коэффициентов (см. подраздел 5.4). Поскольку z П.1 = z П.2, то, как это следует из выражения (5.51), величины A и B должны равняться бесконечности. Следовательно, заданный ЦФ в параллельной форме нереализуем.
