Взяв производную от обеих частей равенства (2), получим

Рисунок 6

Вычислим теперь изгибающий момент в сечении с абсцис­сой 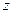, взяв сумму моментов сил, приложенных слева от сечения. Для этого распределенную нагрузку на участке длиной 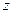заме­няем ее равнодействующей, равной , и приложенной в середи­не участка, на расстоянии 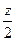от сечения:

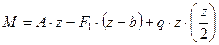. (а)

Аналогичновычислим изгибающиймомент в смежномсече­нии, отстоящем от левой опоры на расстоянии :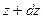

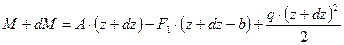(б)

Вычитая (а)из (б), получаемприращение изгибающего момента

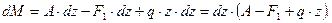
Выражение вскобках представляет собой поперечнуюси­лу 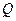. Следовательно,

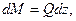
откуда

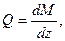(2)

т.е. производная от изгибающего момента по абсциссе сечения балки равна поперечной силе (теорема Журавского).

(3)