ДК включает НКС + УПС приема и передачи.
Алфавит ДК состоит из двух сообщений “1” и “0”.
Основными характеристиками ДК являются:
1. Скорость передачи информации R [бит/с].
2. Скорость модуляции B [Бод].
3. Верность передачи информации характеризуется коэффициентом ошибок по единичным элементам.
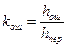 – экспериментально измеряемая величина kош является оценкой для вероятности ошибки –
– экспериментально измеряемая величина kош является оценкой для вероятности ошибки – 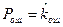 .
.
Статистика ошибок в ДК.
Случайный процесс возникновения ошибок описывается:
1. Заданием входного А и выходного 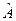 алфавитов.
алфавитов.
2. Совокупностью переходных вероятностей 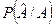 ,
,
где А – произвольный символ (последовательность входного алфавита);
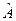 - произвольный символ (последовательность выходного алфавита).
- произвольный символ (последовательность выходного алфавита).
Говорят 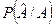 - вероятность приема символа
- вероятность приема символа 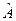 при условии передачи А.
при условии передачи А.
Для расчета переходных вероятностей 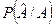 , любых последовательностей конечной длины существуют математические модели ошибок в дискретном канале.
, любых последовательностей конечной длины существуют математические модели ошибок в дискретном канале.
Дискретный симметричный канал без памяти.
Это канал, для которого в любой момент времени вероятность появления символа на выходе зависит только от символа на входе.

Рисунок 1.15 – Диграмма (граф) переходов
вероятность ошибки
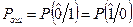 .
.
Вероятности правильного приема
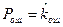
Если эти вероятности заданы, то легко получить вероятность любой последовательности на выходе, зная последовательность на входе 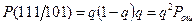 .
.
Определение вероятности ошибок кратности t в принятой последовательности
Положим, что приемником принята последовательность длиной n- элементов.
Вероятность безошибочного приема
 |
(1.11)
Вероятность что ошибка только в 1ом элементе
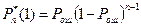 (1.12)
(1.12)
Такая же вероятность будет и для ошибки во втором разряде.
ЗНАЧИТ! Для получения вероятности того, что среди n принятых элементов содержится одна ошибка (на любом месте), нужно просуммировать вероятности всех возможных комбинаций с ошибкой в одном разряде. Таких комбинаций будет n.
Для определения вероятности t ошибок в n-элементной комбинации, в любом сочетании, нужно определить вероятность одного, заданного сочетания ошибок веса t

Затем, умножить данную вероятность на количество всех возможных сочетаний ошибок данного веса.
 |
(1.13)
Тогда окончательно:
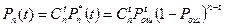 (1.14)
(1.14)
 2014-02-13
2014-02-13 1042
1042








