Теорема 3.6: Пусть 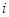 – фиксированная строка определителя
– фиксированная строка определителя 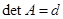 , тогда
, тогда 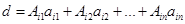 , (то есть определитель равен сумме произведений элементов
, (то есть определитель равен сумме произведений элементов 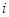 -ой строки определителя на их алгебраические дополнения).
-ой строки определителя на их алгебраические дополнения).
Замечание: Данная теорема позволяет свести вычисление определителя  -го порядка к вычислению определителя
-го порядка к вычислению определителя 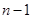 -го порядка. Причем, используя свойства определителя, можно получить в некоторой строке определителя все нули, кроме одного элемента.
-го порядка. Причем, используя свойства определителя, можно получить в некоторой строке определителя все нули, кроме одного элемента.
Теорема Лапласа: Пусть в определителе 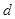 порядка
порядка  выбраны
выбраны 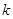 строк (или
строк (или 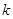 столбцов),
столбцов), 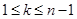 . Тогда сумма произведений всех миноров
. Тогда сумма произведений всех миноров 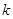 -го порядка, содержащихся на пересечении выделенных строк, на их алгебраические дополнения равна
-го порядка, содержащихся на пересечении выделенных строк, на их алгебраические дополнения равна 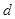 .
.
 2014-02-13
2014-02-13 1374
1374
