Тема 4 Системы линейных уравнений

Рассмотрим систему из 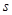линейных уравнений с неизвестными :

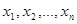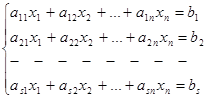, (1)

где 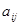– коэффициент, который находится при 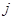-ом неизвестном в 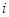-ой строке.

Определение 4.1: Решением системы уравнений (1) называется всякий упорядоченный набор из чисел (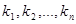) такой, что при подстановке в уравнения системы (1) вместо 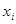чисел 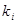получаются верные числовые равенства.

Определение 4.2: Две системы линейных уравнений называются равносильными, если множества их решений равны.

Определение 4.3: Система (1) называется несовместной, если множество ее решений есть пустое множество.

Определение 4.4: Если система (1) имеет только одно решение, то она называется определенной. Если система (1) имеет более одного решения, то она называется неопределенной. Определенные и неопределенные системы называются совместными.

Перечислим элементарные преобразования системы (1), в результате которых будут получаться системы, равносильные данной:

1. Перестановка любых двух уравнений системы.

2. Перенумерация неизвестных системы.

3. Прибавление к одному уравнению системы другого уравнения, умноженного на некоторое число.

Это элементарные преобразования, используемые при решении системы (1) методом последовательного исключения неизвестных (метод Гаусса).