1. Коммутативность сложения:  .
.
2. Ассоциативность сложения: 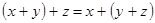 .
.
3. Существует нулевой элемент 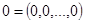 такой, что
такой, что 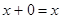 ,
, 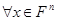 .
.
4. 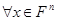 существует единственный противоположный элемент
существует единственный противоположный элемент 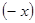 такой, что
такой, что 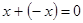 и
и 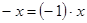 .
.
5. 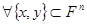 и
и  выполняется:
выполняется:
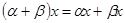
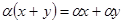
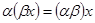
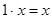 .
.
Определение 5.3: Пусть 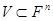 . Множество
. Множество 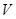 называется линейным подпространством пространства
называется линейным подпространством пространства 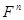 , если множество
, если множество 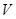 замкнуто относительно операций сложения и умножения на число, то есть
замкнуто относительно операций сложения и умножения на число, то есть 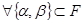 и
и 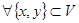
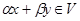 .
.
Определение 5.4: Пусть дана система векторов 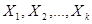 из
из 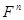 . Будем говорить, что вектор
. Будем говорить, что вектор 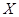 является линейной комбинацией данных векторов, если существуют такие числа
является линейной комбинацией данных векторов, если существуют такие числа 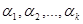 из
из 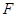 , что
, что  .
.
Определение 5.5: Рассмотрим множество всевозможных линейных комбинаций векторов 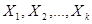 . Это множество называется линейной оболочкой этих векторов и обозначается
. Это множество называется линейной оболочкой этих векторов и обозначается 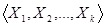 ,
,
то есть
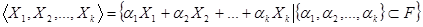 ,
,
и является линейным подпространством.
Определение 5.6: Пусть  – произвольная система векторов из
– произвольная система векторов из 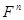 (не обязательно конечная). Рассмотрим всевозможные линейные комбинации векторов из
(не обязательно конечная). Рассмотрим всевозможные линейные комбинации векторов из  –
– 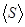 .
. 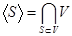 , где
, где 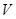 – линейные подпространства.
– линейные подпространства.
Теорема 5.1: 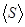 – минимальное линейное подпространство, содержащее систему векторов
– минимальное линейное подпространство, содержащее систему векторов  .
.
 2014-02-13
2014-02-13 553
553








