Правило Крамера
Лемма 4.1: Пусть дано 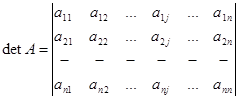 .
.
Рассмотрим произвольные числа 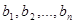 , тогда сумма
, тогда сумма 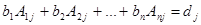 равна определителю, полученному из
равна определителю, полученному из 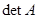 заменой
заменой 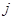 -го столбца на столбец из чисел
-го столбца на столбец из чисел 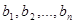 .
.
Следствие: 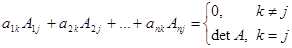 .
.
Правило Крамера: Рассмотрим систему (1). Если 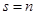 и
и 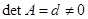 , то система (1) является определенной и
, то система (1) является определенной и 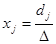 , (
, (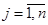 ).
).
Обозначим через 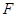 множество вещественных или комплексных чисел, (
множество вещественных или комплексных чисел, ( или
или  ).
).
Рассмотрим упорядоченные  -ки элементов из множества
-ки элементов из множества 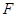 :
: 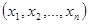 , где
, где 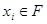 ,
, 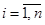 . Эти
. Эти  -ки называются строками (или столбцами) размерности
-ки называются строками (или столбцами) размерности  и образуют множество
и образуют множество 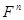 , (
, (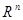 или
или 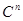 ).
).
Определение 5.1: Пусть 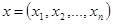 ,
, 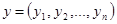 ,
, 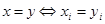 ,
, 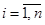 .
.
Введем во множестве 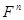 две операции:
две операции:
1. Сложение: 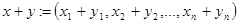 .
.
2. Умножение на число 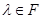 :
: 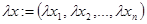 .
.
Определение 5.2: Множество 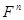 с введенными выше операциями сложения и умножения на число называется
с введенными выше операциями сложения и умножения на число называется  -мерным векторным пространством. Элементы этого пространства будем называть векторами.
-мерным векторным пространством. Элементы этого пространства будем называть векторами.
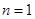 :
: 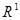 – множество вещественных чисел.
– множество вещественных чисел.
 :
: 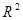 – множество точек плоскости
– множество точек плоскости 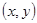 .
.
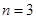 :
: 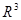 – множество точек пространства
– множество точек пространства 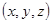 .
.
 2014-02-13
2014-02-13 558
558








