Разложение группы по подгруппе

Пусть 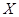– группа.

Определение 9.10: , , .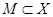

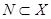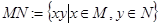Пусть 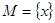, 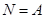– подгруппа группы .

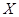Определение 9.11: 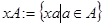называется левым смежным классом (или классом смежности) элемента 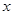по подгруппе , (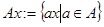– правый смежный класс).

Свойства смежных классов

1. Любой смежный класс 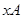полностью определяется любым своим элементом, то есть если 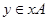, то .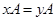

2. Классы смежности по данной подгруппе либо совпадают, либо не пересекаются.

3. Всякая группа равна объединению всех смежных классов, построенных по некоторой ее подгруппе.

Определение 9.12: Пусть множество различных смежных классов по подгруппе группы 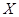будет 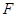, обозначим их 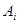. Тогда 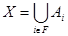называется разложением группы 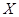по подгруппе .

Теорема Лагранжа: В конечной группе порядок любой подгруппы является делителем порядка самой группы.

Следствие 1: Порядок любого элемента конечной группы является делителем порядка группы.

Следствие 2: Конечная группа, порядок которой есть простое число, является циклической.