2014-02-13
1406
Корни полиномов. Схема Горнера
Алгоритм Евклида
Применяя последовательно теорему о делении с остатком, получим:
,
,
,
……………………………
,
,
,
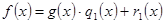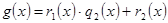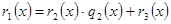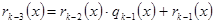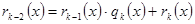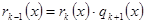где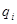 
(
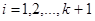) – частные, а 
(
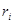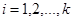) – остатки.
Теорема 8.3: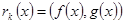 
.
Определение 8.7: Число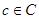 
называется корнем полинома 
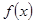, если 
.
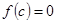Теорема 8.4: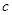 
– корень 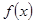тогда и только тогда, когда 
.
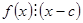Пусть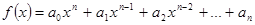 
и
,
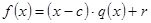где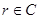 
, 
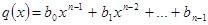, тогда по схеме Горнера:
, 
, 
.
.
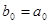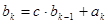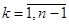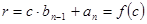Определение 8.8: Есл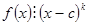и 
и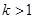 
, то есть 
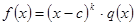, а 
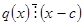, то 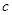называется корнем кратности 
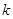полинома .
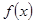Если 
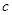, то говорят, что – простой корень .
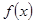Определение 8.9: Пусть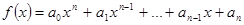 
, тогда 
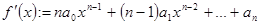называется производной полинома .
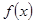Выполняются обычные правила дифференцирования суммы и произведения.
Теорема 8.5: Число 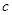является корнем кратности 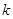для 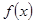тогда и только тогда, когда 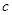– корень кратности 
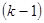для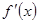 
.
Непрерывность полиномов как функций комплексного переменного
Определение 8.10: Функция 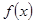, действующая из 
в называется непрерывной в точке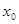 
, если 
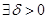такое, что из неравенства 
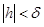следует: 
, 
.
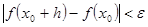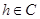Определение 8.11: Функция, непрерывная в произвольной точке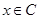 
называется непрерывной.
Лемма: Пусть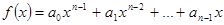 
, 
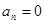. Тогда 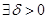такое, что из неравенства 
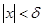следует, что 
.
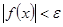Теорема 8.6: Полином 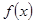является непрерывной функцией комплексного переменного 
.
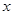Следствие: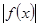 
является непрерывной функцией комплексного переменного.
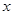Лемма о модуле старшего члена полинома: Пусть дан полином 
-ой степени, 
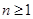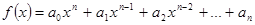. , тогда для любого 
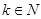существует 
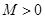такое, что 
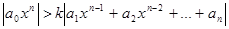, если 
.
Лемма о возрастании модуля полинома: Если 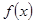– полином степени 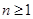, то для любого 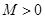существует 
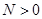такое, что 
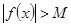при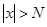 
.
Лемма Даламбера: Если 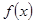– полином степен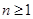и и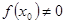 
, то существует 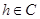такое, что 
.
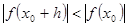Теорема 8.7: Если функция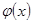 
действует из в 
и непрерывна в замкнутом круге на комплексной плоскости, то 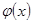достигает в этом круге свое минимальное значение, то есть существует 
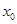из круга такое, что 
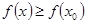для всех 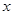из круга.
Основная теорема высшей алгебры: Для любого полинома степени 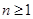существует хотя бы один комплексный корень.
Следствие 1: Если 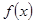– полином степени 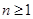, то существуют комплексные числа 
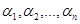, такие, что 
, (
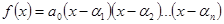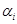могут повторяться).
Следствие 2: Любой полином степени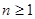 
имеет ровно корней, если каждый корень считать столько раз, какова его кратность.
Следствие 3: Два полинома 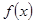и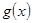 
равны (по определению 8.2) тогда и только тогда, когда 
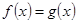для любого .
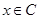Следствие 4 (формула Виета):
Пусть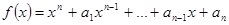 
, , 
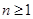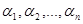– корни полинома, тогда
,
,
,
……………………………………………….
,
.
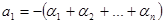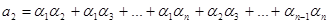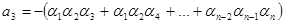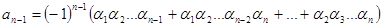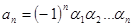Например, при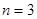 
, получаем:
,
,
.
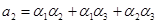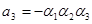Следствие 5: Если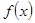 
– полином с вещественными коэффициентами и 
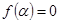, то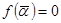 
.
Следствие 6: Всякий полином с вещественными коэффициентами можно разложить на произведение полиномов первой и второй степени с вещественными коэффициентами.
Определение 9.1: Непустое множество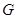 
элементов произвольной природы называется группой, если в нем определена одна алгебраическая операция 
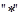, которая обладает следующими свойствами:
1. Ассоциативность: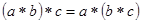 
, 
.
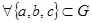2. Операция 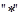обратима, то есть 
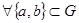существуют единственные 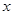и 
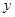из 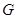такие, что 
, 
.
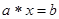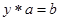Определение 9.2: Группа, состоящая из конечного числа элементов называется конечной, а число элементов в ней – порядком группы.
Определение 9.3: Если групповая операция 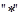коммутативна, то есть 
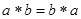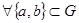, , то группа называется коммутативной или абелевой.
Замечание: Если групповая операция обозначается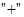 
и называется сложением, то такая форма записи группы называется аддитивной, а если 
и называется умножением – то мультипликативной.
Будем в дальнейшем использовать мультипликативную форму записи группы.
