1. Если 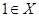 , а
, а 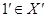 , то
, то 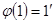 .
.
2. 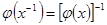 .
.
Определение 9.17: 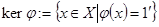 называется ядром гомоморфизма
называется ядром гомоморфизма  .
.
Теорема 9.10: 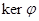 , где
, где  – гомоморфизм, является нормальным делителем группы
– гомоморфизм, является нормальным делителем группы 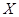 .
.
Определение 9.18: Пусть  – гомоморфизм
– гомоморфизм 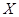 на
на 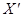 ,
, 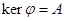 . Поставим в соответствие каждому
. Поставим в соответствие каждому 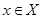 тот класс смежности, в который он входит по факторгруппе
тот класс смежности, в который он входит по факторгруппе 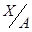 . Это соответствие является гомоморфизмом и называется естественным гомоморфизмом.
. Это соответствие является гомоморфизмом и называется естественным гомоморфизмом.
Теорема о гомоморфизмах: Пусть  – гомоморфизм
– гомоморфизм 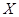 на
на 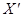 ,
,  . Тогда группа
. Тогда группа 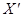 изоморфна факторгруппе
изоморфна факторгруппе 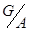 , причем существует такое изоморфное отображение
, причем существует такое изоморфное отображение 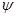 первой из этих групп на вторую, что результат последовательного выполнения отображений
первой из этих групп на вторую, что результат последовательного выполнения отображений  и
и 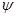 совпадает с естественным гомоморфизмом группы
совпадает с естественным гомоморфизмом группы 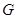 на факторгруппу
на факторгруппу 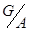 .
.
 2014-02-13
2014-02-13 397
397







