Определение 9.13: Подгруппа  группы
группы 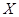 называется ее нормальным делителем, если для любого элемента
называется ее нормальным делителем, если для любого элемента 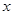 из
из 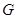 выполняется:
выполняется: 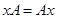 .
.
Теорема 9.7: Подгруппа  группы
группы 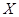 является ее нормальным делителем тогда и только тогда, когда
является ее нормальным делителем тогда и только тогда, когда 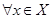 и
и 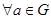 существуют
существуют 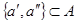 такие, что
такие, что 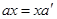 и
и 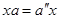 .
.
Определение 9.14: Элемент  из группы
из группы 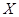 называется сопряженным элементу
называется сопряженным элементу 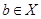 , если существует
, если существует 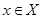 такой, что
такой, что 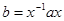 .
.
Теорема 9.8: Подгруппа  группы
группы 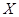 является ее нормальным делителем тогда и только тогда, когда
является ее нормальным делителем тогда и только тогда, когда  содержит все элементы, сопряженные к своим элементам, то есть
содержит все элементы, сопряженные к своим элементам, то есть 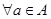 и
и 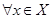 ,
, 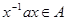 .
.
Следствие: Если  и
и 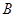 – нормальные делители группы
– нормальные делители группы 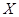 , то
, то 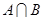 – нормальный делитель группы
– нормальный делитель группы 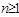 .
.
 2014-02-13
2014-02-13 927
927








