a) Подынтегральная функция представляет собой несократимую правильную рациональную дробь. Кроме того, знаменатель разложен на простейшие множители. Заметим, что все корни знаменателя действительные: 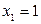 - двукратный корень,
- двукратный корень, 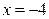 - простой корень.
- простой корень.
Разложим подынтегральную функцию в сумму простейших дробей:
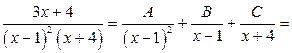
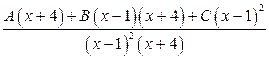 . (2.7)
. (2.7)
Поскольку в (2.7) дроби, стоящие слева и справа, равны и имеют одинаковые знаменатели, то должны быть равны и их числители:
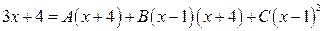 . (2.8)
. (2.8)
Подставим в равенство (2.8) вместо 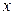 последовательно значения корней знаменателя:
последовательно значения корней знаменателя:
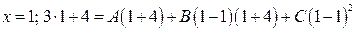 ;
;
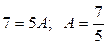 ;
;
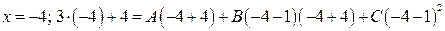 ;
;
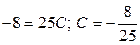 .
.
Подставим теперь в (2.8) вместо 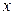 любое значение, например,
любое значение, например, 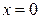 :
:
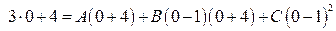 ;
;
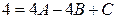 ;
;
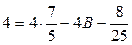 ;
;
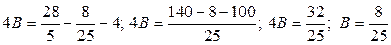 .
.
Следовательно, 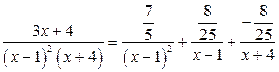 и
и
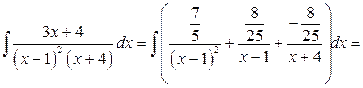
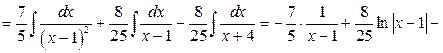
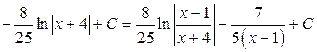 .
.
Вспомогательные вычисления:
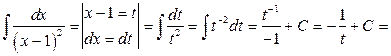
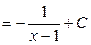 .
.
б) Подинтегральная функция является неправильной рациональной дробью. Поэтому сначала выделим целую часть:

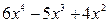
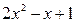


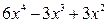
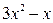

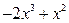

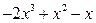

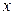
Результат деления можно записать в виде
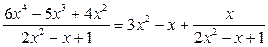 .
.
Тогда
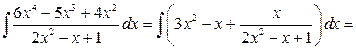
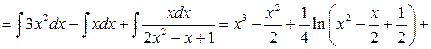
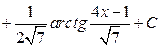
Вспомогательные вычисления.
Выделим сначала полный квадрат двучлена:
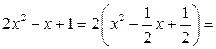
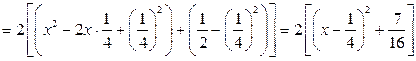 .
.
Тогда
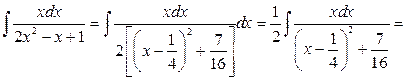
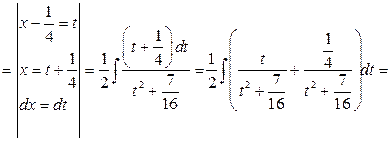
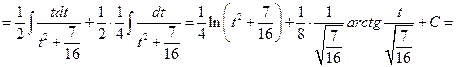
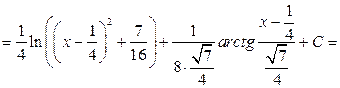
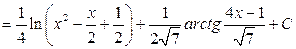 .
.
В заключение отметим, что алгоритм нахождения неопределенного интеграла от рациональной дроби можно кратко сформулировать следующим образом:
1) выделение целой части, если дробь неправильная, т.е. представление ее в виде суммы многочлена и правильной рациональной дроби;
2) разложение знаменателя на простейшие множители с действительными коэффициентами в случае, если он не представлен в виде разложения;
3) интегрирование многочлена;
4) представление полученной правильной рациональной дроби в виде суммы простейших дробей;
5) интегрирование полученного разложения правильной дроби;
6) запись конечного результата суммированием интеграла от многочлена и интеграла от правильной рациональной дроби.
► Найти интегралы:
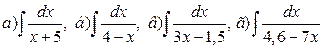 .
.
► Выделите полный квадрат двучлена из трехчлена:
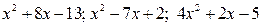 .
.
► Опишите метод замены переменной.
► Найти интегралы:
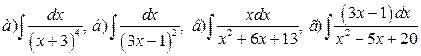 .
.
Ответы: а) 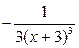 ; б)
; б) 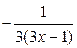 ;
;
в) 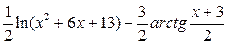 ;
;
г) 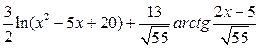 .
.
► Найти интегралы:
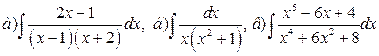 .
.
Ответы: а) 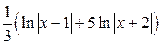 ; б)
; б) 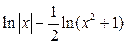 ;
;
в) 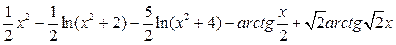 .
.
 2015-05-13
2015-05-13 653
653








