Дробно-рациональной функцией или рациональной дробью 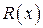 называется отношение двух многочленов:
называется отношение двух многочленов: 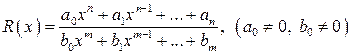 .
.
Если степень многочлена в числителе меньше степени многочлена в знаменателе, т.е. 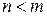 , то рациональная дробь называется правильной. В противном случае рациональная дробь называется неправильной.
, то рациональная дробь называется правильной. В противном случае рациональная дробь называется неправильной.
Интегрирование дробно-рациональной функции проводится в несколько этапов. Сначала мы перечислим эти этапы, а потом подробно поясним каждый из них на примере. Итак, для интегрирования дробно-рациональной функции 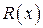 следует:
следует:
1) если рациональная дробь неправильная, то выделить из нее целую часть и правильную рациональную дробь 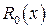 :
: 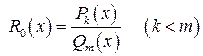 ;
;
2) знаменатель дроби 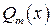 разложить на линейные множители
разложить на линейные множители 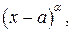
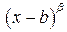 , и квадратные множители
, и квадратные множители 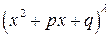 , с действительными коэффициентами;
, с действительными коэффициентами;
3) правильную рациональную дробь разложить методом неопределенных коэффициентов на простейшие дроби
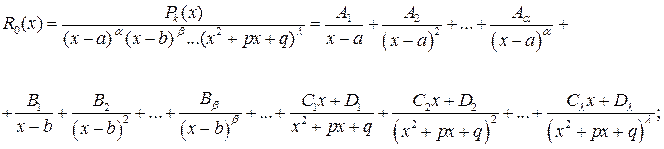
4) найти неопределенные (неизвестные пока) коэффициенты
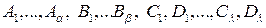 ;
;
5) найти интегралы от целой части и простейших дробей.
Поясним все сказанное на примерах.
Пример 4. Найти интеграл 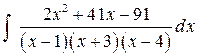 .
.
Подынтегральная функция есть правильная рациональная дробь, так как степень многочлена в числителе меньше степени многочлена в знаменателе. Кроме того, знаменатель уже разложен на линейные множители. Поэтому сразу переходим к разложению рациональной дроби на простейшие дроби с неопределенными коэффициентами:
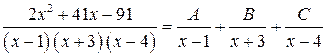 .
.
Умножив это равенство на 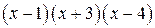 , получим:
, получим:
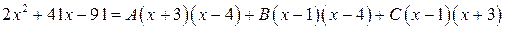 .
.
Подставив в это равенство последовательно 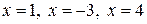 , получим
, получим 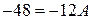 ,
, 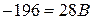 ,
, 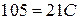 . Таким образом,
. Таким образом, 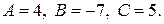
Мы нашли коэффициенты разложения 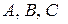 методом частных значений.
методом частных значений.
Теперь подставим найденные значения 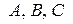 в равенство:
в равенство:
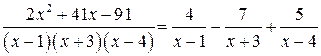 .
.
Проинтегрируем полученные простейшие дроби:
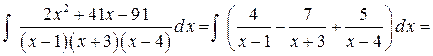

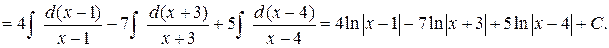
Пример 5. Найти интеграл 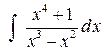 .
.
Подынтегральная функция есть неправильная рациональная дробь, так как степень многочлена в числителе больше степени многочлена в знаменателе. Поэтому выделим из неправильной дроби ее целую часть, поделив числитель на знаменатель.
В результате деления получим:
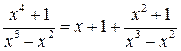 .
.
Теперь знаменатель получившейся правильной дроби разложим на множители 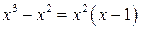 , а саму правильную дробь на простейшие дроби:
, а саму правильную дробь на простейшие дроби:
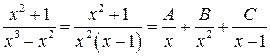 .
.
Умножив это равенство на 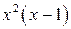 , получим:
, получим:
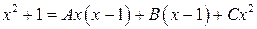 .
.
Подставив в это равенство значения 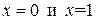 , получим
, получим 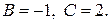
Для отыскания коэффициента 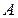 можно либо в равенстве (14.5) подставить еще одно частное значение
можно либо в равенстве (14.5) подставить еще одно частное значение  , либо в правой и левой частях равенства (14.5) приравнять коэффициенты при одинаковых степенях
, либо в правой и левой частях равенства (14.5) приравнять коэффициенты при одинаковых степенях  , например, при
, например, при  :
: 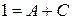 .
.
Тогда 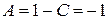 . Подставляя найденные
. Подставляя найденные 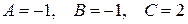 в равенство (14.4) и используя равенство (14.3), окончательно получим
в равенство (14.4) и используя равенство (14.3), окончательно получим
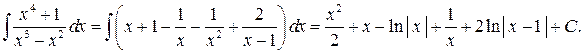
Пример 6. Найти интеграл 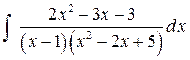 .
.
Подынтегральная функция есть правильная рациональная дробь, так как степень многочлена в числителе меньше степени многочлена в знаменателе. Квадратный трехчлен в знаменателе 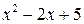 имеет отрицательный дискриминант, следовательно, он не имеет действительных корней и не разлагается на линейные множители с действительными коэффициентами. Поэтому перейдем к разложению рациональной дроби на простейшие:
имеет отрицательный дискриминант, следовательно, он не имеет действительных корней и не разлагается на линейные множители с действительными коэффициентами. Поэтому перейдем к разложению рациональной дроби на простейшие:
 .
.
Умножив это равенство на  , получим
, получим
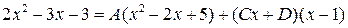 .
.
Подставив в это равенство значения 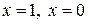 получим:
получим:
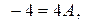
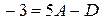 или
или 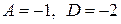 .
.
Кроме того, в правой и левой частях равенства сравним коэффициенты при  :
: 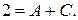 Итак,
Итак, 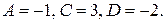 Используя равенство, получим
Используя равенство, получим
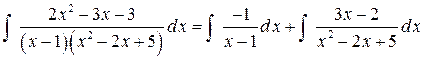 .
.
Найдем первый интеграл: 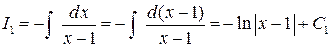 .
.
Для отыскания второго интеграла выделим в числителе производную квадратного трехчлена, стоящего в знаменателе:
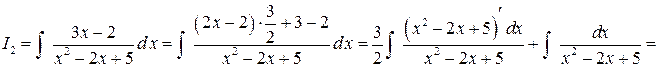
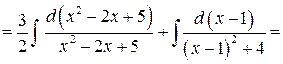
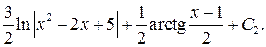
Складывая 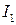 ,
, 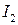 и вводя
и вводя 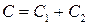 , получим искомый интеграл:
, получим искомый интеграл:
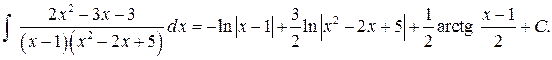
Пример 7. Найти интеграл 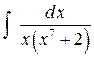 .
.
Здесь разложение знаменателя на линейные и квадратичные множители и разложение дроби на простейшие требуют громоздких выкладок. Значительно проще вынести из скобки 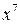 :
: 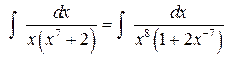
и воспользоваться тем, что 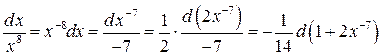 .
.
Тогда 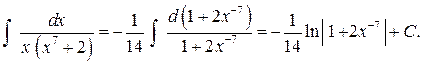
Пример 8. Найти интеграл 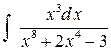 .
.
Решение. Как и в предыдущем примере, разложение знаменателя на линейные и квадратичные множители и разложение дроби на простейшие требуют громоздких выкладок. Удобнее воспользоваться тем, что 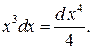 Тогда
Тогда
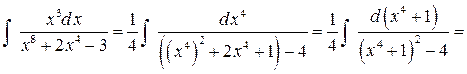
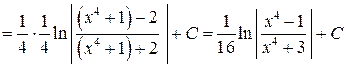 .
.
 2014-02-02
2014-02-02 14745
14745
