Линейная система n-порядка устойчива, если при изменении частоты ω от 0 до +∞ характеристический вектор системы D(jω) повернется против часовой стрелки на угол n·π/ 2, необращаясь негде в 0.
Система устойчива, если при кривая Михайлова начинаясь при ω=0 на действительной положительной полуоси проходит при изменении частоты ω от 0 до +∞ последовательно против часовой стрелки n квадрантов комплексной плоскости.
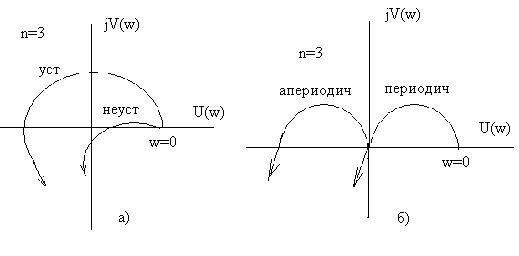
Система находится на апериодической границе устойчивости, если кривая Михайлова при ω=0 начинается в начале координат и на колебательной границе, если при ω≠0 кривая проходит через начало координат.
Число правых корней ХУ системы равно числу неправильных пересечений кривой Михайлова с осями координат
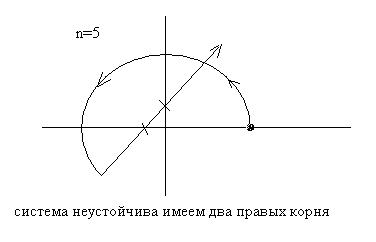
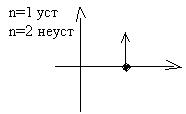
Примечание: кривая Михайлова образует развертывающую спираль, поэтому обычно ее строят не в масштабе, а лишь фиксируя пересечения с осями.
ЛЕКЦИЯ №8
Пример: Оценить устойчивость системы по критерию Михайлова 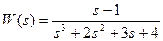
ХУ: 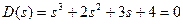 (по Гурвицу сразу видно, что система устойчива).
(по Гурвицу сразу видно, что система устойчива).
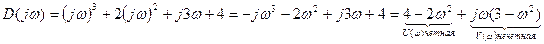
| ω | U(ω) | V(ω) |
| ∞ 1.41 1.73 | -∞ -2 | -∞ 1.41 |
U(ω)=0 → 4-2ω2=0 → ω=√2
V(ω)=0 → 3-ω2=0 → ω=√3
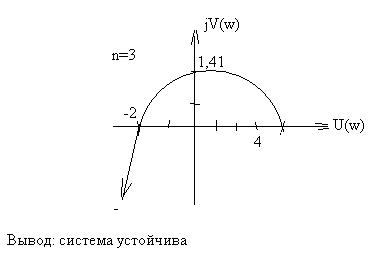
Cледствие: 2 форма критерия Михайлова
Система устойчива, если четная U(ω) и нечетная V(ω) функции при изменении ω от 0 до +∞ обращаются в нуль поочередно т.е. их корни перемежаются (чередуются).

 2014-02-13
2014-02-13 649
649








