Уравнение Шредингера является одним из фундаментальных уравнений современной физики – это основное уравнение нерелятивистской квантовой механики

Получить уравнение Шредингера можно из следующих соображений.

Пусть в момент времени 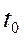задана волновая функция .

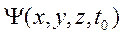В некоторый момент времени 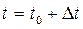(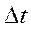достаточно мало). В первом приближении из разложения в ряд Тейлора

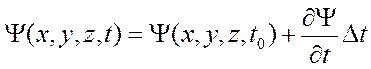
Пользуясь понятием оператора, можно записать

.

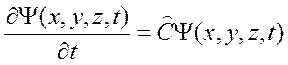Требуется определить вид оператора .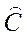

Приведенное выражение должно быть справедливым для плоской волны де Бройля

.

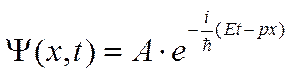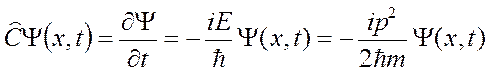, т.к. .

.

.

.

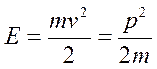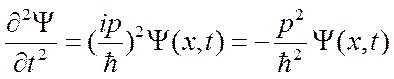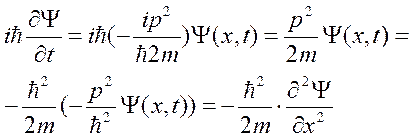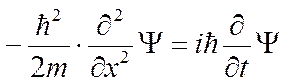Последнее уравнение – это уравнение Шредингера для свободной частицы.

Для свободной частицы

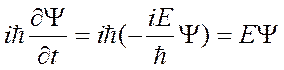, или .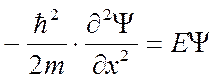

Оператор 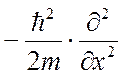сопоставляется энергии свободной частицы при одномерном движении,

т.е. 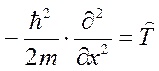- это оператор кинетической энергии.

Для связанной частицы энергия ,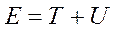

Потенциальной энергии сопоставляется операторпотенциальной энергии .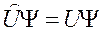

Для несвободной частицы уравнение Шредингера сохраняет свой вид, только вместо оператора кинетической энергии фигурирует оператор полной энергии 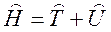(оператор Гамильтона), т.е. для связанной частицы

.

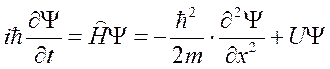В трехмерном случае

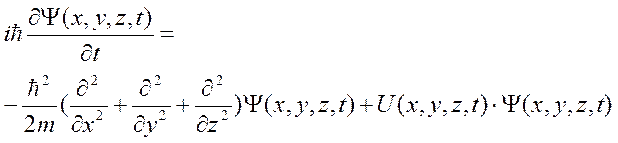
это общее уравнение Шредингера.

Оператор 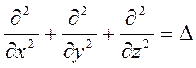- оператор Лапласа (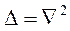, где 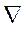- оператор набла).

В таком случае общее уравнение Шредингера запишется в виде

.

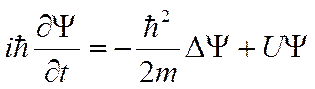Это уравнение позволяет определять волновую функцию микрочастицы (т.е. характеристику микрочастицы) в любой момент времени, если эта функция известна в начальный момент времени.