2014-02-17
1991
Решением уравнения Шредингера является комплексная волновая функция (например, для свободной частицы 
).
Уравнение Шредингера – это дифференциальное уравнение.
Поэтому для однозначности решения надо определить постоянные интегрирования. Для этого необходимо задать начальные условия -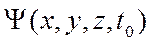 
и граничные условия, т.е. значения 
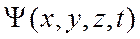на границах области (например, на 
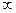). Таким образом, постановка задачи включает в себя не только задание 
, но и задание начальных и граничных условий.
Из физического содержания волновой функции и математических требований к уравнению Шредингера вытекают естественные (стандартные) условия:
· функции должны быть непрерывными,
· однозначными и конечными во всех точках,
· первые производные функции также должны быть непрерывными и конечными.
Однозначность пси-функции следует из физического смысла функции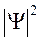 
. Требование конечности пси-функции следует из условия нормировки:
,
т.е. вероятность обнаружения частицы в ограниченном пространстве конечна (не больше 100%).
Волновая функция 
несет всю информацию о свойствах системы. Она служит средством для описания физических явлений. Поэтому y-функция, как решение уравнения Шредингера, должна удовлетворять следующим требованиям:
1) она должна быть совместной с соотношениями
; 
; 
;
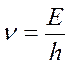2) она должна быть линейной относительно возможных решений уравнения Шредингера
;
3) функция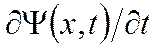 
также должна быть линейной;
Уравнение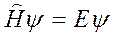 
в общем случае может иметь множество решений. Из всех возможных решений выбирают только такие, для которых соответствующие волновые функции удовлетворяют стандартным условиям.
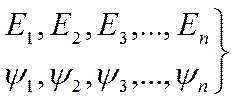
- это и есть решение уравнения Шредингера.
Из уравнения Шредингера для стационарных состояний и стандартных условий для волновой функции непосредственно вытекает квантование энергии микрочастицы.
Для стационарных состояний в ограниченном пространстве спектр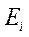 
является дискретным (т.е. энергия квантуется).
Функции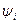 
, удовлетворяющие уравнению 
, называют собственными функциями оператора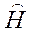 
, а значения 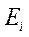- собственными значениями.
Собственные функции оператора Гамильтона являются ортогональными, т.е.
, если 
.
Если специально выбрать множитель А у функции таким образом, чтобы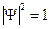 
, то функции 
будут ортонормированными (т.е. ортогональными и нормированными одновременно). В этом случае можно записать:
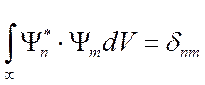, где 
символ Кронекера.
Каковы рамки применимости уравнения Шредингера?
1-е ограничение – уравнение Шредингера справедливо только для нерелятивистской микрочастицы (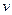
<<
).
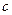2-е ограничение – уравнение Шредингера не учитывает существование собственного механического момента микрочастиц – спина.
В 1929 г. П.Дирак разработал основы релятивистской квантовой механики, одним из результатов которой явилось подтверждение существования спина микрочастиц.
