2014-02-17
724
Таблица
Решение
Исходные данные
| Среднемесячный доход, руб. | Численность, чел. |
| до 500 | |
| 500 – 1000 | |
| 1000 – 1500 | |
| 1500 – 2000 | |
| 2000 – 2500 | |
| свыше 2500 | |
| Итого |
Построить теоретический закон распределения в предположении, что случайная величина Х (генеральная совокупность) распределена по нормальному закону.
Так как параметры нормального распределения (a, σ) неизвестны, то заменим их соответствующими несмещенными и состоятельными точечными оценками (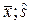
). Рассчитаем выборочную среднюю и выборочное среднее квадратическое отклонение[5].
| Интервалы[ хi; хi+1 ] | Середина интервала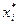 
| ni |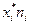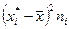 
| 
|
| до 500 | 40006028,896 | |||
| 500 – 1000 | 67301998,568 | |||
| 1000 – 1500 | 17065497,424 | |||
| 1500 – 2000 | 13860721,690 | |||
| 2000 – 2500 | 63745442,342 | |||
| свыше 2500 | 47281486,049 | |||
| Итого | - | 249261174,968 |
.
.
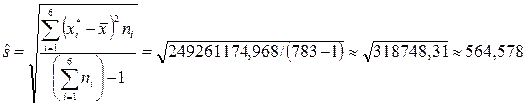С учетом рассчитанных точечных оценок параметров распределения функция плотности вероятностей и функция распределения будут иметь соответственно следующий вид:
|
|
|
,
.
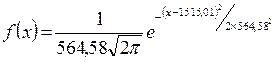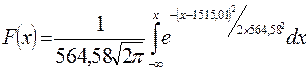При формировании статистического распределения выборки используются частоты, определенные по выборочным данным, поэтому их называют также эмпирическими.
При построении теоретического закона распределения исследуемой случайной величины используют теоретическиечастоты, т.е. частоты определенные расчетным способом.
Рассмотрим механизм расчета теоретических частот для дискретных и непрерывных случайных величин.
