Электроны, двигающиеся по инерции вдоль замедляющей системы, подвергаются действию продольной составляющей высокочастотного поля Ez. Исходя из концепции точечных электронов, применим к одиночному электрону обычное уравнение динамики:
По правилам дифференцирования функций нескольких переменных, имеем:
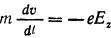
Отбрасывая произведение малых величин, получаем:
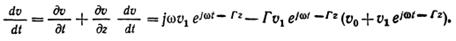
Таким образом, уравнение движения электронов позволяет вычислить переменную составляющую скорости электронов в пучке:
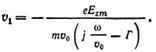
Вычислим плотность конвекционного тока в пучке в присутствии бегущей волны. Плотность тока J находим как произведение объемной плотности зарядов на их скорость.
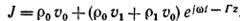
Таким образом, переменная составляющая плотности конвекционного тока в пучке равна
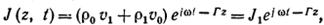
где J1 — амплитуда плотности конвекционного тока:
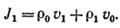
По уравнению непрерывности заряда:
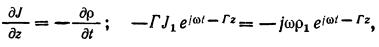
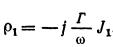
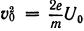
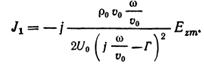
Величину — имеющую размерность фазовой постоянной неко го
торой волны, двигающейся с фазовой скоростью, равной v0, в дальнейшем будем называть электронным волновым числом:
|
|
|
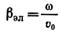
Величина p0v0 = J0 является постоянной составляющей плотности тока в пучке. Таким образом, уравнение для переменной составляющей плотности конвекционного тока приобретает окончательный вид
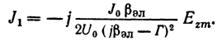
Отсюда, учитывая площадь сечения пучка, переходим к амплитуде полного конвекционного тока:
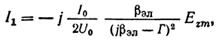
где I0 — постоянная составляющая тока пучка. Конвекционный ток электронного пучка в комплексной форме имеет вид
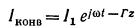
 2014-02-09
2014-02-09 864
864








