1) Напомним, что суперпозицию двух и более функций мы называем также сложной функцией.
Теорема. Пусть функция  определена на интервале
определена на интервале 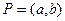 , а функция
, а функция 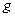 определена на интервале
определена на интервале 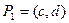 , причем
, причем 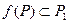 . Тогда если функция
. Тогда если функция  дифференцируема в точке
дифференцируема в точке 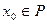 , а функция
, а функция 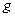 дифференцируема в точке
дифференцируема в точке 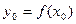 , то сложная функция
, то сложная функция 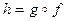 дифференцируема в точке
дифференцируема в точке  и
и
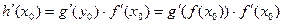
| (1) |
Д о к а з а т е л ь с т в о. В силу дифференцируемости функций  и
и 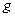 , соответственно, в точках
, соответственно, в точках  и
и 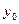 , имеем
, имеем
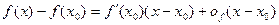
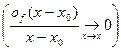
| (2) |
и
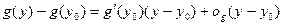
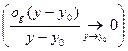
| (3) |
Как известно
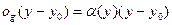 , ,
| (4) |
где 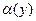 - бесконечно малая при
- бесконечно малая при 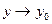 , причем без ущерба для общности можно считать, что
, причем без ущерба для общности можно считать, что 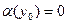 , то есть можно считать, что функция
, то есть можно считать, что функция 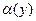 непрерывна в точке
непрерывна в точке 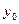 .
.
Из (3) и (4) следует, что
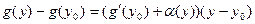
Подставляя сюда 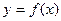 ,
,  и используя затем равенство (2), получим
и используя затем равенство (2), получим
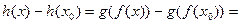
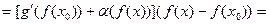
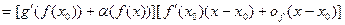
и, следовательно,
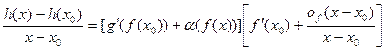
| (5) |
Поскольку функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция 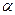 непрерывна в точке
непрерывна в точке 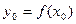 и
и 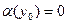 , то по теореме о непрерывности сложной функции
, то по теореме о непрерывности сложной функции
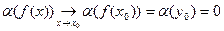 .
.
А так как, кроме того,
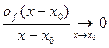
то из (5) следует, что существует конечная производная
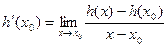
и имеет место равенство (1). Для завершения доказательства теоремы остается вспомнить, что существование конечной производной 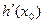 равносильно дифференцируемости функции
равносильно дифференцируемости функции 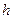 в точке
в точке  .
.
Замечание. Пусть выполнены условия теоремы. Тогда по определению дифференциала
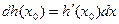
| (6) |
И, в силу равенства (1), для сложной функции будем иметь
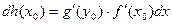
или
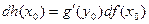
| (7) |
Считая точку  произвольной (то есть заменяя
произвольной (то есть заменяя  на произвольное
на произвольное 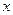 ). Равенства (6) и (7) записывают в виде
). Равенства (6) и (7) записывают в виде
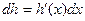
| (6¢) |
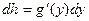
| (7¢) |
Эти формулы показывают, что формально вид дифференциала не меняется как при записи его через независимую переменную 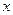 , так и при записи через зависимую переменную. В этом состоит, так называемое, свойство инвариантности дифференциала, который называют также первым дифференциалом.
, так и при записи через зависимую переменную. В этом состоит, так называемое, свойство инвариантности дифференциала, который называют также первым дифференциалом.
 2014-02-09
2014-02-09 554
554








