2014-02-09
855
Пусть на интервале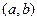 
заданы функции
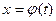
| (1) |
и
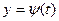
| (2) |
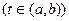. Предположим, что функция 
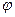строго монотонна на 
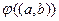. Тогда она имеет обратную функцию
,
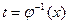которая является строго монотонной на промежутке 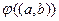. Рассмотрим функцию
 ,
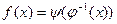| (3) |
называемую функцией, заданной параметрически уравнением (1) и (2). При этом, отметим, параметром называют переменную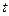 
функций 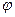и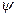 
.
Теорема. Пусть функци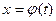и и 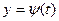определены на интервале 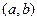и дифференцируемы в точке 
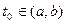, причем функция 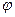строго монотонна на 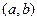и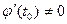 
. Тогда функция 
, заданная параметрически уравнениями (1) и (2), дифференцируема в точке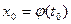 
и
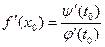
| (4) |
Д о к а з а т е л ь с т в о. Дифференцируемость функции в точке 
имеет место в силу теоремы о дифференцируемости обратной функции и теоремы о дифференцируемости сложной функции. Из тех же теорем вытекает и формула (4). Действительно, по теореме о дифференцируемости сложной функции
 ,
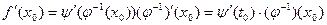| (5) |
а по теореме о дифференцируемости обратной функции
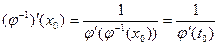
| (6) |
Из (5) и (6) имеем (4)
