2014-02-09
733
Прежне всего напомним, что всякая строго монотонная функция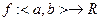 
имеет обратную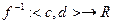 
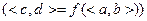, которая строго монотонна в том же смысле, что и “прямая” функция. При этом обратная функция будет непрерывной на промежутке 
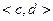, если прямая строго монотонная функция непрерывна на промежутке 
.
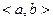Теорема. Пусть функция 
строго монотонна и непрерывна в окрестности 
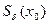точки 
. Пусть, кроме того, функция дифференцируема в точке и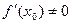 
. Тогда обратная к ней функция 
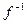дифференцируема в точке 
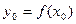, причем
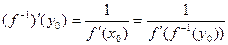
| (1) |
Д о к а з а т е л ь с т в о. Из условий теоремы следует, что существует конечный, отличный от нуля предел
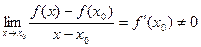
Тогда по теореме о пределе частного существует конечный предел
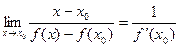
| (2) |
Рассмотрим функцию
 .
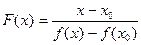| (3) |
В силу строгой монотонности функции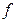 
она определена в проколотой окрестности 
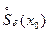точки . В точке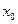 
функция 
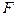имеет конечный предел (2). Поэтому если доопределить ее в этой точке равенством
,
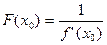то она будет непрерывной в этой точке. Тогда учитывая, что функция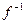 
непрерывна в точке 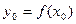(как обратная к непрерывной, строго монотонной функции 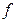), по теореме о непрерывности суперпозиции заключаем, что сложная функция 
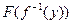будет непрерывной в той же точке 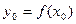и, следовательно,
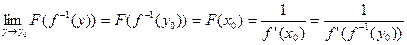
| (4) |
Поскольку в некоторой проколотой окрестност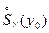и 
точки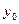 
в силу равенства (3) имеет место равенство
,
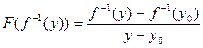и предел функции в данной точке не зависит от того, как она определена в этой точке, то из (4) следует, что функция 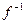дифференцируема в точке 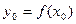и имеют место равенства (1) □
