Скалярное произведение векторов
Опр. Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними: 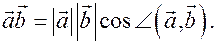
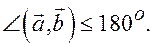
1. 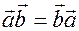 (очевидно из определения).
(очевидно из определения).
2.  , то есть числовой множитель можно выносить за знак скалярного произведения.
, то есть числовой множитель можно выносить за знак скалярного произведения.
∆ 

а) 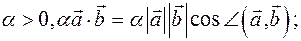 Правые части равны,
Правые части равны,
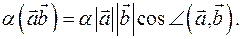 значит, равны и левые.
значит, равны и левые.
б) 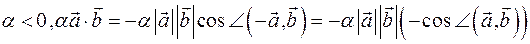 ,
,

И в этом случае правые части равны, значит, равны и левые. Свойство доказано.
3. 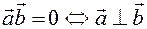 (признак перпендикулярности векторов).
(признак перпендикулярности векторов).
4. Скалярный квадрат вектора равен квадрату его модуля:

5. Скалярное произведение векторов 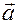 и
и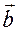 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 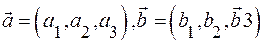 , выражается формулой:
, выражается формулой: 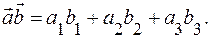
∆ Пусть 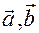 не нулевые и не коллинеарные векторы. Отложим их от одной точки пространства.
не нулевые и не коллинеарные векторы. Отложим их от одной точки пространства.
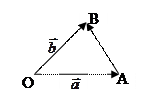 Применим к
Применим к 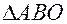 теорему косинусов:
теорему косинусов:
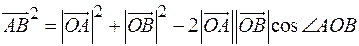 ,
, 
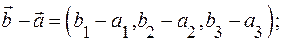

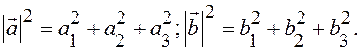 Подставляя в равенство
Подставляя в равенство  получим:
получим:

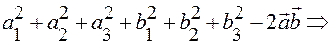
 ▲
▲
Задача. Рассмотрите случай 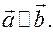
6.  При доказательстве используется свойство 5.
При доказательстве используется свойство 5.
7. 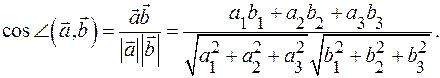
 2014-02-09
2014-02-09 701
701








