Линейные операции над векторами

К линейным относятся операции сложения и вычитания векторов и умножения вектора на число.

2.1. Сложение векторов

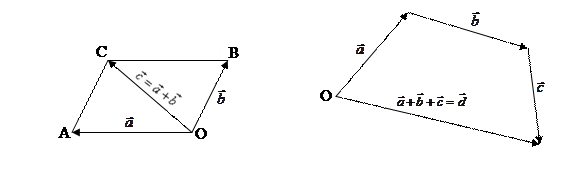
Правило треугольника

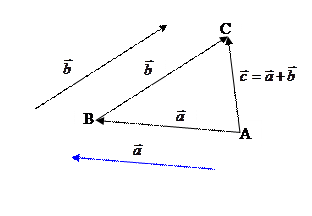Сумма векторов: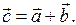

Как видно, здесь строится .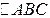

Для любых трех точек А, В и С справедливо равенство:

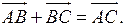
Правило параллелограмма Правило многоугольника

Теорема 1. Сложение векторов обладает свойствами:

1.

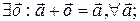
2.

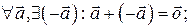
3. (коммутативность сложения);

4. 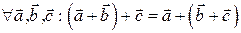(ассоциативность сложения).

∆ 1.Пусть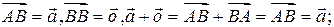

2.Пусть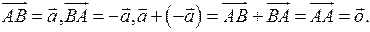

3.Смотри правило параллелограмма.

4. Смотри правило многоугольника:

▲

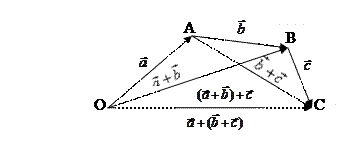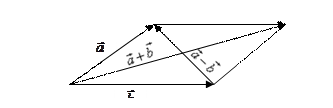
2.2..Вычитание векторов

Опр. Разностью двух векторов 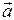и 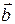называется вектор 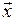такой, что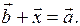

Найдем вектор 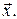Для этого прибавим к обеим частям последнего равенства вектор:

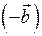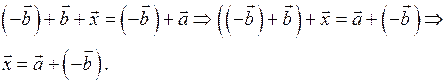
Итак, разность векторов всегда существует. Её обозначают так:

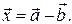
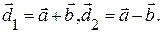
2.3. Умножение вектора на число

Пусть 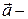некоторый вектор, 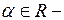вещественное число.

Опр. Произведением вектора 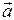на число 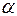называется такой вектор 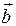, который удовлетворяет условиям:

1)

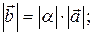
2) 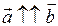, если ,

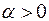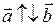, если .

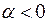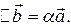
Условиями 1) и 2) вектор 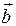определяется однозначно.

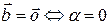или 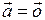, то есть 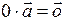и .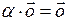

Теорема 2. Умножение вектора на число обладает свойствами:

1.

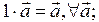
2.

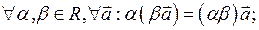
3.

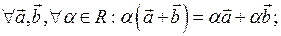
4. .

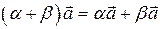∆ Докажем первые два свойства.

1. Обозначим 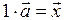и покажем, что .

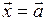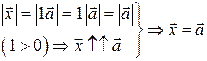, то есть .

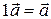2. Обозначим .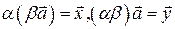

Векторы 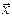и 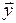имеют одну и ту же длину.

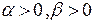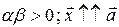Возможны случаи:

и 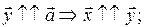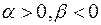и

и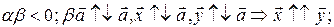

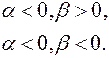И т.д.

Направления векторов 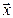и 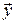всегда совпадают, длины их равны. Следовательно, ▲

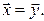2.4. Векторные пространства

Рассмотрим все множество 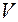векторов и определим в нем линейные операции сложения и умножения на число. Такое множество называется линейным пространством, если при этом выполняются условия 1-4 для сложения и 1-4 для умножения на число.

Примеры векторных пространств: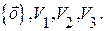

Множество вещественных квадратных матриц 2-го порядка является 4-мерным линейным пространством.