2014-02-09
1212
Раздел 2. Метод координат на плоскости
Базис на плоскости образует любая пара неколлинеарных векторов
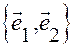. Отложим эти векторы от определенной точки О.
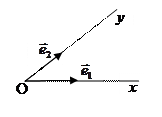Тройка 
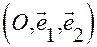называется аффинной системой
координат на плоскости (или обобщенной декартовой
системой координат), или аффинным репером.
Точка О – начало координат,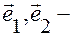 
координатные векторы, прямая вектора 
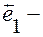ось абсцисс, прямая вектора 
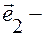ось ординат.
Пусть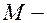 
точка на плоскости, 
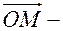её радиус-вектор.
Опр. Координатами точки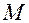 
называются координаты её радиуса-вектора
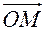в базисе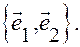 
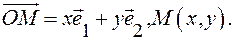
Итак, каждой точке 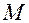на плоскости соответствует пара действительных чисел 
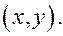Обратно: каждой упорядоченной паре чисел 
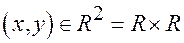(декартов квадрат множества действительных чисел) соответствует определенная точка на плоскости с координатами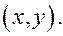
Таким образом, после введения аффинной системы координат на плоскости устанавливается взаимно однозначное соответствие между точками плоскости и парами чисел из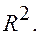 
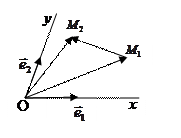
Пример. Постройте точку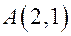 
и вектор 
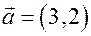в данной системе координат.
Задача. В аффинной системе координат даны две точки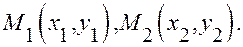 
Найдите координаты вектора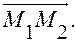 
∆ 
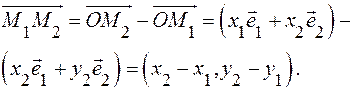
Вывод. Координаты вектора равны разности соответствующих координат конца и начала. ▲
