Алгоритм приведения общего уравнения линии
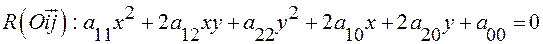
1. Составим характеристическое уравнение:
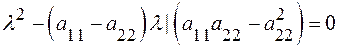
и найдем его корни.
2. Совершим поворот данной системы координат на угол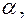 определяемый по формуле:
определяемый по формуле:
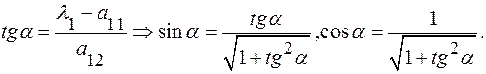
Формулы преобразования координат: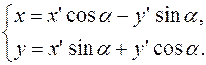
3.Запишем уравнение кривой в новой системе координат 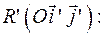
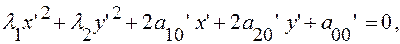 (*)
(*)
где 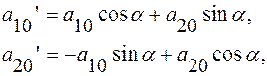
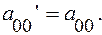
4.Совершив параллельный перенос системы координат, получим из уравнения (*) каноническое уравнение кривой в системе 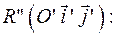
5. Построим системы 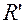 и
и 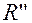 и по каноническому уравнению данную
и по каноническому уравнению данную
линию.
Пример. Преобразованием прямоугольной системы координат приведите уравнение линии второго порядка 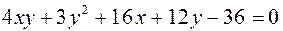 к каноническому виду.
к каноническому виду.
Решение
1. Запишем и решим характеристическое уравнение кривой:
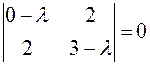 , отсюда
, отсюда 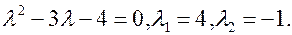
2. Находим угол поворота системы координат:
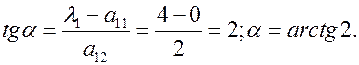
Тогда cos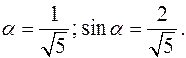
3. Запишем формулы преобразования координат при повороте системы координат на угол 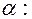
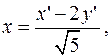
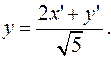
4. После поворота осей координат уравнение линии запишется в виде:
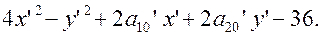
Найдем коэффициенты 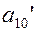 и
и 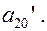
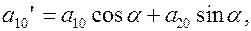
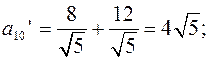
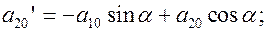
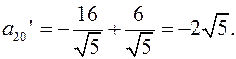
Уравнение принимает вид:
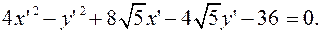
5.Преобразуем уравнение, используя параллельный перенос осей в новое начало.
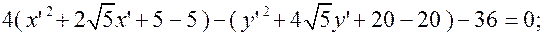
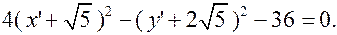
Выполним параллельный перенос системы координат в точку 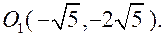
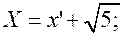
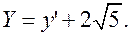
Уравнение кривой запишется в виде: 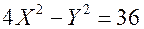 или
или 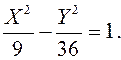
Получили каноническое уравнение гиперболы.
Построение графика
1. Строим исходную систему координат Оху.
2. Поворачиваем Оху на угол 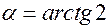 ,
,
получим систему О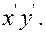
3. Переносим 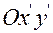 параллельно в точку
параллельно в точку 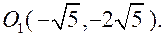
Получим систему 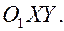
4. В последней системе строим гиперболу 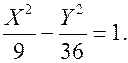
 2014-02-09
2014-02-09 685
685








