Плоскость
Раздел 3. Система координат в пространстве
 1.1.1.Параметрические уравнения плоскости.
1.1.1.Параметрические уравнения плоскости.
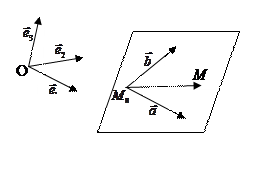
Положение плоскости 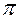 в пространстве
в пространстве
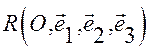 определим заданием
определим заданием
точки  и двух неколлинеарных
и двух неколлинеарных
векторов 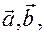 которым плоскость
которым плоскость 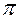
параллельна: 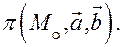
Если точка 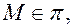 то векторы
то векторы 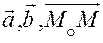 компланарны. Тогда
компланарны. Тогда
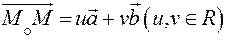 (1)
(1)
Если на плоскости 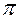 взять аффинную систему координат
взять аффинную систему координат 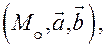 то
то 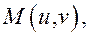
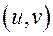 - координаты точки
- координаты точки 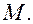
Пусть 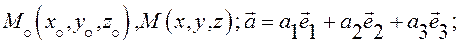
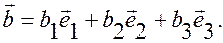 Из соотношения (1) имеем:
Из соотношения (1) имеем:
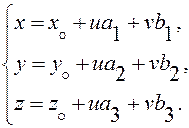 (2)
(2)
Из (1) следует (2), и наоборот.
Уравнения (2) называются параметрическими уравнениями плоскости.
1.1.2. Уравнение плоскости, проходящей через 3 точки.
Зададим в аффинной системе 3 неколлинеарные точки 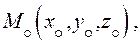
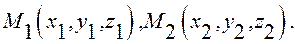 Они определяют единственную плоскость
Они определяют единственную плоскость 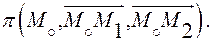 Для произвольной точки
Для произвольной точки 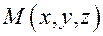 плоскости выполняется условие
плоскости выполняется условие 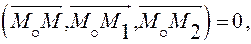 то есть
то есть
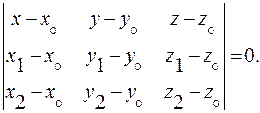 (3)
(3)
1.1.3. Уравнение плоскости «в отрезках»
Возьмем, в частности, в качестве точек 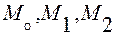 точки пересечения плоскости с осями координат
точки пересечения плоскости с осями координат 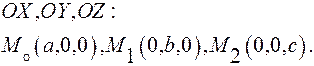
Уравнение (3) принимает вид:
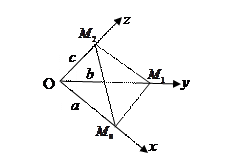
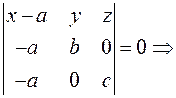
уравнение «в отрезках» 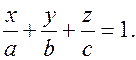 (4)
(4)
1.1.4..Общее уравнение плоскости.
Зададим плоскость 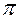 точкой
точкой 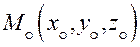 и двумя неколлинеарными векторами:
и двумя неколлинеарными векторами: 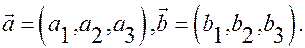 Если
Если 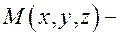 произвольная точка плоскости, то векторы
произвольная точка плоскости, то векторы 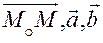
компланарны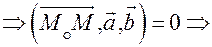
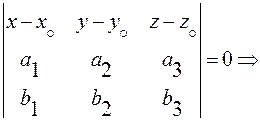
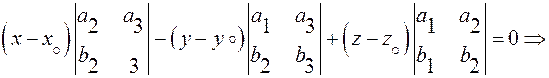
 где
где
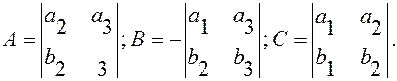
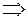
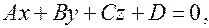 (5)
(5)
где
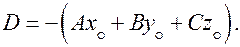
Очевидно, в дпск вектор 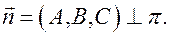
Как видно, в аффинной системе координат плоскость определяется уравнением 1-ой степени относительно трех переменных. Справедливо и обратное утверждение: при 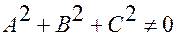 уравнение первой степени относительно 3-х переменных
уравнение первой степени относительно 3-х переменных 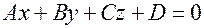 в аффинной системе координат определяет плоскость.
в аффинной системе координат определяет плоскость.
1.1.5.Условие параллельности вектора и плоскости.
Теорема. Для того, чтобы в аффинной системе координат вектор
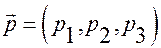 был параллелен плоскости
был параллелен плоскости
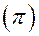
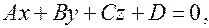
необходимо и достаточно, чтобы выполнялось условие
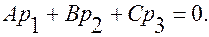 (6)
(6)
∆ 1. Пусть 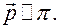 Если точка
Если точка 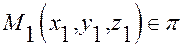 и
и 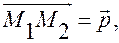 то точка
то точка 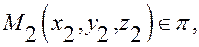 то есть справедливы равенства:
то есть справедливы равенства:
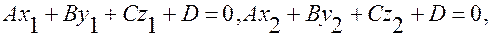
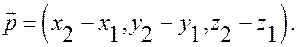 Вычитая из второго третье, получим:
Вычитая из второго третье, получим: 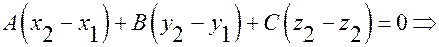
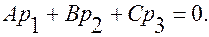
2. Если выполнено условие (6) и точка 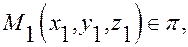 то, если
то, если
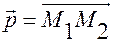 , из
, из 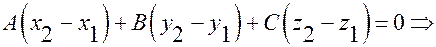
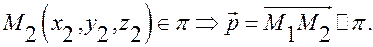 ▲
▲
1.1.6. Неполные уравнения плоскости. Построение плоскости по
уравнению.
Уравнение 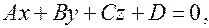 где ни один из коэффициентов не равен 0, называется полным. Для построения плоскости его лучше записать «в отрезках»:
где ни один из коэффициентов не равен 0, называется полным. Для построения плоскости его лучше записать «в отрезках»:
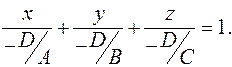
Пример. Постройте плоскость 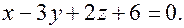
Обратимся к неполным уравнениям, заданным в аффинной системе координат 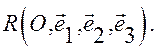
1. 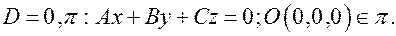
Пример. Постройте плоскость 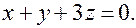
2. 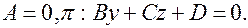 Вектор
Вектор  параллелен плоскости
параллелен плоскости 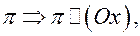 если
если  и
и 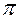 проходит через ось
проходит через ось 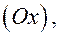
если 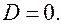
Пример. Постройте плоскость 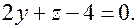
3. 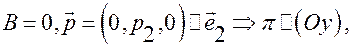 если
если  и
и 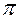 проходит через ось
проходит через ось 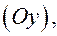 если
если 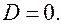
Пример. Постройте плоскость 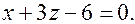
4. Если  то плоскость параллельна оси
то плоскость параллельна оси 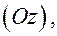 и проходит через эту ось, если
и проходит через эту ось, если 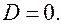
5. 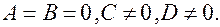 Плоскость
Плоскость 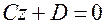 параллельна плоскости
параллельна плоскости 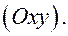
6. 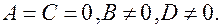 Плоскость
Плоскость 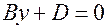 параллельна плоскости
параллельна плоскости 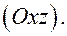
7.  Плоскость
Плоскость 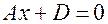 параллельна плоскости
параллельна плоскости 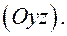
8. 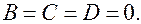 Плоскость
Плоскость 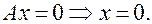 Это координатная плоскость
Это координатная плоскость 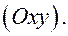
9. 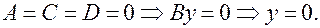 Это плоскость
Это плоскость 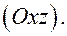
10. 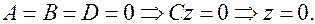 Это плоскость
Это плоскость 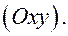
1.1.7. Геометрический смысл знака многочлена 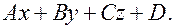
Пусть в аффинной системе координат 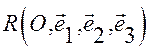 задана плоскость
задана плоскость 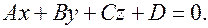 Координаты точек, принадлежащих этой плоскости обращают это уравнение в верное тождество. Плоскость делит пространство на два подпространства. Можно доказать, что для координат точек одного подпространства Значение многочлена
Координаты точек, принадлежащих этой плоскости обращают это уравнение в верное тождество. Плоскость делит пространство на два подпространства. Можно доказать, что для координат точек одного подпространства Значение многочлена 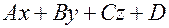 есть положительное число (именно для того подпространства, где находится вектор
есть положительное число (именно для того подпространства, где находится вектор 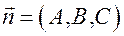 ), а для точек другого подпространства – отрицательное.
), а для точек другого подпространства – отрицательное.
Задача. Определите взаимное расположение точек 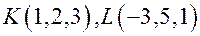 относительно плоскости
относительно плоскости 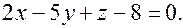
 2014-02-09
2014-02-09 978
978








