2014-02-09
499
a. Угол между плоскостями.
Пусть в дпск заданы две плоскости:
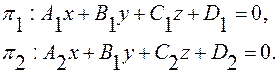
За угол между плоскостями принимается любой из двугранных углов, образованных ими. Он, очевидно, равен углу между их нормальными векторам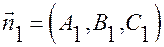и: 
и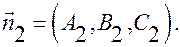 
Следовательно, угол между плоскостями определяется по формуле:
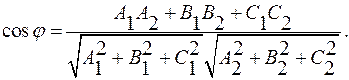(9)
Условие параллельности плоскостей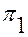 
и 
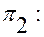
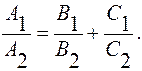(10)
Условие перпендикулярности плоскостей 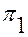и
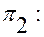
(11)
Задача. Через точку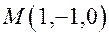 
провести плоскость, параллельную плоскости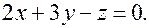 
3.2.Расстояние от точки до плоскости.
Пусть в дпск заданы плоскость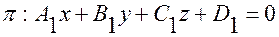 
и точка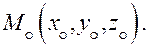 
Найдем расстояние 
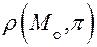от точки до плоскости. Пусть 
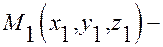основание перпендикуляра, опущенного из точки 
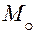на плоскость.
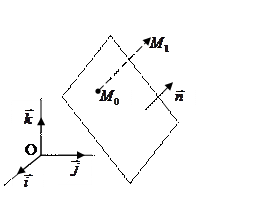Нормальный вектор 
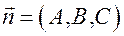плоскости и
вектор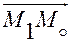 
коллинеарны. Найдем их
скалярное произведение:
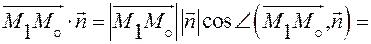
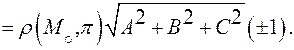
Вычислим левую часть этого равенства, учитывая, что
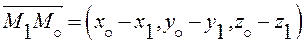. Получим:
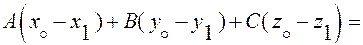
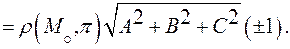
Раскрывая скобки в левой части и учитывая, что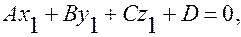 
так как 
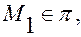получим окончательно:
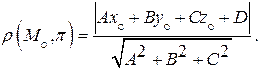(12)
Задача. Найдите расстояние между плоскостями: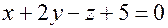 
и
