2014-02-09
958
Линейная антенна
На новее полученных простых соотношений мы будем теперь рассматривать более общий случай: линейную антенну, на длину которой не накладывается никаких ограничений, она может быть сопоставима с длиной волны, больше ее и т.д. Причем, в отличие от диполя Герца, у такой антенны распределение тока вдоль ее длины может быть произвольным. Например, для бесконечно тонкой антенны с длиной, лежащей в пределах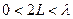 
, распределение тока может быть аппроксимировано следующим выражением: 
.
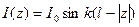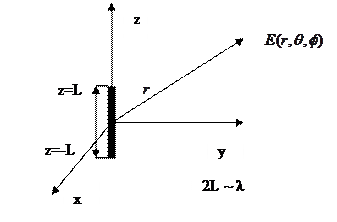
Рис. 4.1.Линейная антенна с произвольным токовым распределением
Установим связь между произвольным распределением тока и полем излучения такой антенны в дальней зоне. Для этого представим антенну как последовательность соединенных друг с другом диполей Герца длины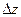 
:
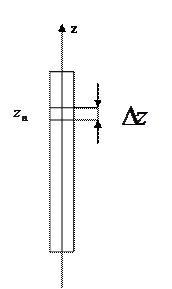
Рис. 4.2.
Тогда электрическое поле в дальней зоне мы можем записать следующим образом:
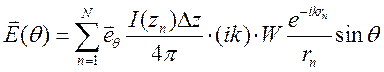
где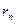 
- расстояние между точкой наблюдения и диполем Герца с номером n. Теперь устремим n к бесконечности, тогда вместо суммы мы получим определенный интеграл:
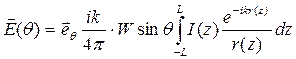. (4.1.)
Здесь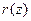 
-текущее расстояние между точкой на антенне с координатой 
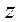и точкой наблюдения. Теперь воспользуемся тем обстоятельством, что точка наблюдения находится в дальней зоне (
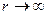), поэтому можно приближенно считать, что все линии, проведенные от любой точки на антенне к точке наблюдения параллельны друг другу. Проведем в точку наблюдения прямую из центра излучателя длиной 
.
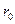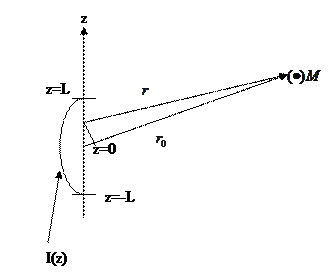
Рис. 4.3.К выводу выражения для поля излучения линейной антенны
Сравним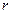 
и 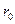. Так как мы рассматриваем случай в дальней зоне, то это позволяет утверждать, что прямые 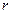и 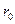в первом приближение параллельны (хотя, строго говоря, это не так). Рассмотрение прямоугольного треугольника позволяет связать 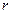и :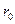
.
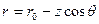Данное приближение работает только в дальней зоне. Подставим это выражение в показатель экспоненты интеграла (4.1.). С точки зрения абсолютной величины 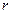и 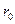практически равны, но с точки зрения разности фаз волн, приходящих в точку наблюдения от различных элементов антенны, равенства не наблюдается. И действительно: 
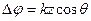=> если L=λ/2, то 
.
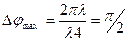В знаменателе подинтегрального выражения небольшие вариации расстояния 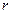совершенно несущественно скажутся на амплитуде поля в дальней зоне. В итоге запишем:
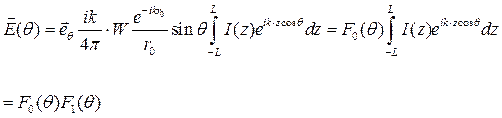(4.2.)
где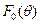 
- диаграмма направленности диполя Герца, 
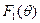- множитель системы.
Выводы:
1) Электрическое поле представляет собой произведение двух функци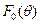й и 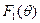, первая из которых 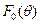- диаграмма направленности диполя Герца, а 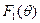- множитель, который учитывает размеры и способ возбуждения антенны. Данный вывод является содержанием теоремы перемножения.
2) Связь между напряженностью поля в дальней зоне и распределением тока носит интегральный характер. Множитель системы представляет собой преобразование Фурье от функции распределения тока. Покажем это:
Дополним функцию распределения тока: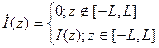 
. Далее введем замену переменных: 
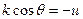. В итоге получим: 
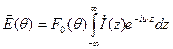- это выражение с точностью до коэффициента совпадает с преобразованием Фурье. Из доказанного выше утверждения следует, что все известные свойства преобразования Фурье можно перенести на антенную технику. В частности одно из важнейших положений связывает электрические размеры антенны и ширину ее главного лепестка.
