Метод дерева решений

Тема 6. Выбор наилучшей альтернативы в условиях риска на основе дерева решений

Как правило, на практике ЛПР имеет дело не с набором альтернатив, для которых уже известны их параметры, а с постановкой задачи в условиях риска, заданной в развернутой форме на содержательном уровне и нуждающейся в формализации. При этом требуется формализовать не только сами альтернативы, но и различные возможные варианты для сочетания доходов и потерь при реализации определенных случайных событий, не зависящих от ЛПР. Иными словами, содержание задачи включает в себя структуру взаимосвязанных между собой альтернатив и возможных случайных событий, которую необходимо описать формально для нахождения наилучшего решения при заданном отношении ЛПР к риску.

Такая формализация и структуризация задачи, а также поиск наиболее предпочтительной для ЛПР альтернативы с учетом его отношения к риску могут быть реализованы на основе метода дерева решений. Данный метод позволяет синтезировать имеющиеся альтернативы и случайные события с учетом конкретных параметров и представить их структуру в виде графа специального вида, называемого деревом решений (то есть граф без циклов).

Граф состоит из вершин и соединяющих их ребер (либо дуг). Он строится следующим образом. Для его начальной (корневой) вершины существует набор различных цепей (каждая из которых характеризует определенную возможную траекторию развития рассматриваемого процесса), приводящих к концевой вершине. Концевая вершина отражает экономический результат такой отдельной траектории цепи. Различают вершины прямоугольного и круглого типов.

Вершина прямоугольного типа отражает ситуацию, обусловливаемую необходимостью выбора одной альтернативы непосредственно самим ЛПР из некоторого множества имеющихся альтернатив (например, выбор типа транспорта, выбор конкретного маршрута и т.д.). Ребра, исходящие из такой вершины, отражают возможности такого выбора в виде определенных альтернатив (например, морской транспорт, автотранспорт и т.д.). При этом альтернативы могут и должны быть представлены с указанием конкретных значений параметров, значимых для расчетов при реализации такой траектории развития процесса.

Вершина круглого типа представляет собой определенный фактор, воздействие которого на рассматриваемый процесс имеет случайный характер и не зависит от ЛПР. Исходящие из такой вершины ребра соотносятся с набором рассматриваемых случайных сценариев, влияющих на конечный экономический результат, вероятности реализации которых должны быть известны.

Каждая траектория (цепь от корневой вершины к концевой вершине дерева решений) приводит к конечной вершине, которая может быть представлена как конкретное числовое значение экономического результата, либо как его случайная величина с известным законом распределения.

Для иллюстрации рассмотрим некоторое простейшее дерево решений, состоящее из одной вершины прямоугольного типа, двух вершин круглого типа и четырех концевых вершин. Его структура представлена на рис 6.1.

Как видно на рис. 6.1., исходящие из прямоугольной вершины ребра оканчиваются однотипными вершинами (круглого типа), имеющими по две концевые вершины. Такая идентичность связана с тем, что при реализации каждой из двух альтернатив (рассматриваемого множества) необходимо всякий раз учитывать воздействие случайного фактора отмеченного типа Т, характеризуемого двумя сценариями. Подчеркнем, что общем случае число рассматриваемых сценариев может быть произвольным. Соответственно, это определит и число концевых вершин. При этом конкретные значения для показателя конечного экономического результата концевых вершин в общем случае будут различными.

Процедура параметризации дерева решений подразумевает соотнесение параметров альтернатив и случайных сценариев исходной задачи с соответствующими вершинами и ребрами построенного графа.

На рис. 6.2. представлено дерево решений после реализации процедуры параметризации, причем отражено следующее. Рассматриваются альтернативы А₁ и А₂, случайный фактор имеет два сценария реализации Т₁ и Т₂. Здесь T₁ наступает с вероятностью p₁, а T₂ - с вероятностью p₂. Соответственно, концевые вершины отражают конкретные числовые значения дохода:

· D₁₁ – при выборе первой альтернативы и реализации первого случайного сценария (при А₁ и Т₁),

· D₁₂ – при выборе первой альтернативы и реализации второго случайного сценария (А₁ и Т₂),

· D₂₁ – при выборе второй альтернативы и реализации первого случайного сценария (А₂ и Т₁),

· D₂₂ – при выборе второй альтернативы и реализации второго случайного сценария (А₂ и Т₂).

Процедура свертки предусматривает для вершин круглого типа «замену» исходящих из них ребер, отражающих распределение вероятностей конечного результата, на определенный набор параметров, соответствующих критерию выбора при заданном отношении ЛПР к риску.

Представим основные критерии, которые используют для выбора наилучшей альтернативы. В теории риска такими критериями являются EVC – критерий и MVC - критерий.

При нейтральном отношении к риску при оптимизации решения используют EVC – критерий ожидаемого значения (the expected value criterion). Тогда менеджеру необходимо найти только математическое ожидание рассматриваемых вероятностных распределений, причем наилучшей признается альтернатива с наибольшим математическим ожиданием дохода.

При осторожном отношении к риску применяют MVC - критерий значимой дисперсии (the mean variance criterion). Он требует определения как математического ожидания, так и дисперсии распределения конечного экономического результата. Показатель критерия, который требуется определить, совпадает со значением функции выбора f_s(σ;m) = m – k_s·σ². Наилучшей при этом критерии признается альтернатива с наибольшим значением указанной функции.

Аналогично, при склонности к риску также используется критерий MVC, показатель которого при таком отношении к риску равен значению функции выбора f_r(σ;m) = m + k_r·σ². Наилучшей также является альтернатива с наибольшим значением указанной функции.

Отмеченные выше для использования в формате метода дерева решений критерии формулируются следующим образом:

· Критерий EVC: f_n(σ;m) = m ®max - для нейтральных к риску ЛПР;

· Критерий MVC: f_s(σ;m) = m – k_s·σ² ®max - для осторожных к риску ЛПР;

· Критерий MVC: f_r(σ;m) = m + k_r·σ² ®max - для склонных к риску ЛПР.

Соответственно, процедура свертки подготавливает параметры для выбираемых ЛПР критериев. При этом, в формате заданного отношения к риску в вершину круглого типа вписывается значение соответствующей функции выбора f(σ;m). Для этого рассчитываются необходимые параметры, конкретизирующие расположение альтернативы в пространстве «Риск-Доход».

Заметим, что при нейтральном отношении к риску в формате процедуры свертки менеджеру достаточно сразу вписывать в вершины круглого типа значения математического ожидания распределения конечного экономического результата, как это представлено на рис. 6.3.

.

На рис. 6.3. представлено дерево решений после процедуры свертки при нейтральном отношении к риску, где по формулам теории вероятности найдены соответствующие математические ожидания:

m₁ = p₁·D₁₁+ p₂·D₁₂,

m₂ = p₁·D₂₁+ p₂·D₂₂.

Заметим, что при произвольном количестве (n) концевых вершин, исходящих из рассматриваемой вершины круглого типа, указанные формулы имели бы вид

m₁ = p₁·D₁₁+ p₂·D₁₂ + …+ p_n·D_1n = ;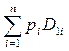

m₂ = p₁·D₂₁+ p₂·D₂₂ + …+ p_n·D_2n = .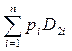

Соответственно, на рис. 6.4. представлено дерево решений после реализации процедуры свертки при осторожном отношении к риску. Здесь

· f_s(m₁,σ₁)= m₁ – k_s·σ₁²,

где m₁ = p₁·D₁₁+ p₂·D₁₂,

σ₁² = m₁⁽²⁾ – (m₁)² = p₁·(D₁₁)²+ p₂·(D₁₂)² – (p₁·D₁₁+ p₂·D₁₂)²,

· f_s(m₂,σ₂)= m₂ – k_s·σ₂²

где m₂ = p₁·D₂₁+ p₂·D₂₂,

σ₂² = m₂⁽²⁾ – (m₂)² = p₁·(D₂₁)²+ p₂·(D₂₂)² – (p₁·D₂₁+ p₂·D₂₂)².

Подчеркнем, что количество концевых вершин (см. рис. 6.2) в формате одного случайного фактора может любым. Поэтому приведем формулы, например, для определения показателя уровня f_s(m₁,σ₁) в таком случае.

В случае n концевых вершин для расчета показателя f_s(m₁,σ₁)= m₁ – k_s·σ₁² имеем:

m₁ =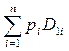

σ₁² = m₁⁽²⁾ – (m₁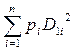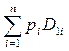)² = – ()².

Формулы для определения f_s(m₂; σ₂) аналогичны.

Наконец, на рис. 6.5. представлено дерево решений после процедуры свертки для склонных к риску ЛПР. Здесь

· f_r(m₁,σ₁)= m₁ + k_r·σ₁²

где m₁ = p₁·D₁₁+ p₂·D₁₂,

σ₁² = m₁⁽²⁾ – (m₁)² = p₁·(D₁₁)²+ p₂·(D₁₂)² – (p₁·D₁₁+ p₂·D₁₂)²,

· f_r(m₂,σ₂)= m₂ + k_r·σ₂²

где m₂ = p₁·D₂₁+ p₂·D₂₂,

σ₂² = m₂⁽²⁾ – (m₂)² = p₁·(D₂₁)²+ p₂·(D₂₂)² – (p₁·D₂₁+ p₂·D₂₂)².

Процедура блокировки требует для вершин прямоугольного типа зачеркнуть (заблокировать) на графе те исходящие из них ребра, которые ведут к заведомо неоптимальным (в формате предпочтений ЛПР) последующим вершинам графа, то есть не имеющим наибольшего значения соответствующей функции выбора. Тем самым исключаются из рассмотрения худшие варианты для траектории развития процесса. Таким образом, после реализации всех указанных процедур остается альтернатива с наибольшим значением функции выбора. Она и является наилучшей для ЛПР при заданном отношении к риску. Процедуры свертки и блокировки проводятся от концевых вершин к начальной вершине.

После завершения процедур свертки и блокировки дерево решений уже будет представлено в таком виде, при котором оптимальное решение становится очевидным. Как следует из рис. 6.6. при нейтральном отношении к риску будет выбрана альтернатива А₁, поскольку m₁> m₂ (она выделена жирным шрифтом).

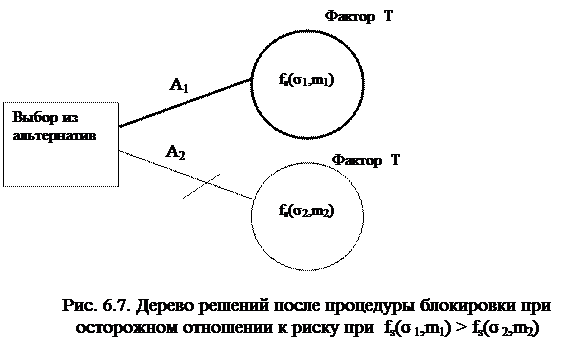
Как следует из рис. 6.7. при осторожном отношении к риску выбор попадает на альтернативу А₁, поскольку f_s(σ₁,m₁) > f_s(σ₂,m₂). Аналогично, при склонности к риску после процедуры блокировки также останется альтернатива с наибольшим значением f_r(σ,m).

Метод дерева решений имеет ряд важных для ЛПР особенностей/преимуществ:

1) Во-первых, менеджер может структурировать рассматриваемую задачу и самостоятельно выбрать наиболее значимые для ЛПР альтернативы и сопутствующие им случайные факторы, влияющие на конечный экономический результат анализируемого процесса.

2) Во-вторых, метод позволяет менеджеру учитывать отношение ЛПР к риску на основе использования функций выбора, которые могут быть формализованы ранее или скорректированы в связи с новыми условиями бизнеса или с учетом соответствующего нового опыта в таком бизнесе.