Аналитическое представление альтернатив и отношения к риску

Тема 5. Сравнение альтернатив в условиях риска

При сравнении альтернатив в условиях риска необходимо учитывать отношение к риску конкретного лица, принимающего решения (далее ЛПР). В формате классического подхода теории риска отношение к риску складывается из субъективного понятия ЛПР относительно имеющегося «баланса» в сочетании возможных случайных значений для доходов и потерь, сопутствующих рассматриваемой альтернативе. Каждая альтернатива характеризуется двумя значимыми для ЛПР показателями: ожидаемый доход, возможный риск. В соответствии с теорией риска ЛПР может выразить свое отношение к риску как осторожное, склонное к риску и нейтральное.

При этом подразумевается, что склонность к риску означает, что ЛПР рассчитывает на такую величину благоприятного отклонения дохода, которая бы компенсировала, возможно, и не вполне достаточный ожидаемый доход.

Осторожность к риску означает, что ЛПР требует такую величину ожидаемого дохода, которая бы могла компенсировать соответствующий риск (в формате возможного отрицательного отклонения конечного экономического результата).

При нейтральном отношении к риску ЛПР ориентируется только на средний ожидаемый конечный экономический результат.

При этом одна и та же альтернатива может не устраивать склонного к риску ЛПР из-за недостаточного дохода и в то же время не устраивать осторожного к риску ЛПР из-за недопустимого риска. Сравнение альтернатив возможно только при заданном отношении к риску, которое должно быть формализовано так, чтобы можно было однозначно выбирать (из набора альтернатив) наилучшую для конкретного ЛПР.

При классическом подходе к риску каждая альтернатива может быть представлена как случайная величина в формате конечного экономического результата (в денежном выражении), которая характеризуется двумя параметрами:

- математическим ожиданием (m);

- среднеквадратическим отклонением (σ).

Математическое ожидание оценивает средний ожидаемый доход альтернативы, а среднеквадратическое отклонение показывает, насколько, в среднем, конечный экономический результат может отклонится в большую или в меньшую сторону от своей средней ожидаемой величины. При классическом подходе к риску величина среднеквадратического отклонения ожидаемого дохода альтернативы принимается как мера ее риска.

При этом некоторая функция ¦, зависящая от указанных параметров (σ;m). вводится таким образом, чтобы критерий выбора имел следующую структуру:

¦(σ;m)®max.

Другими словами, из двух альтернатив предпочтительнее будет альтернатива с большим значением заданной функции выбора.

Математическое ожидание конечного экономического результата рассматриваемой альтернативы воспринимается всегда однозначно: чем больше такой показатель, тем он лучше для ЛПР при любом отношении к риску. В частности, при нейтральном отношении к риску такой показатель выступает как единственный значимый для ЛПР параметр: значение параметра σ не влияет на результат сравнения альтернатив. Восприятие же среднеквадратического отклонения как меры риска различно для осторожного к риску и для склонного к риску ЛПР. Осторожность к риску выражается в том, что чем меньше величина среднеквадратического отклонения дохода альтернативы, тем это лучше для ЛПР (при фиксированном математическом ожидании). Указанное обстоятельство обуславливается стремлением такого ЛПР обеспечить наиболее надежный доход из возможных при заданном его среднем ожидаемом значении. Напротив, склонность риску выражается в том, что чем больше величина среднеквадратического отклонения (σ) дохода альтернативы (при заданном m), тем это лучше для ЛПР. Указанное обстоятельство можно объяснить стремлением сохранить шанс получения наибольшего дохода из возможных, поскольку большая величина среднеквадратического отклонения дохода альтернативы воспринимается склонным к риску ЛПР как возможность отклонения, скорее, в благоприятную сторону.

С учетом указанных особенностей восприятия риска как среднеквадратического отклонения дохода альтернативы, отношение ЛПР к риску характеризуется функцией выбора f(σ;m), которая в простейшем случае может быть формализована, например, следующим образом (представленные ниже функции могут быть заданы и иначе по желанию ЛПР):

· f_n(σ;m) = m - для нейтральных к риску ЛПР;

· f_s(σ;m) = m – k_s·σ² - для осторожных к риску ЛПР;

· f_r(σ;m) = m + k_r·σ² - для склонных к риску ЛПР.

где k_s – коэффициент индивидуальной осторожности ЛПР к риску;

k_r – коэффициент индивидуальной склонности ЛПР к риску;

Соответственно, при нейтральном отношении к риску значение функции выбора совпадает с математическим ожиданием дохода альтернативы. Для осторожного к риску ЛПР в функции выбора учтено его восприятие возможного риска отклонения конечного экономического результата как нежелательного и отрицательного события, при этом дисперсия ожидаемого конечного результата умножается на коэффициент (k_s), который характеризует степень такого осторожного отношения к риску для конкретного ЛПР. Для склонного к риску ЛПР в функции выбора учтено его восприятие возможного риска отклонения (σ) конечного экономического результата как желательного и положительного события (для отклонения в нужную благоприятную сторону), при этом дисперсия ожидаемого конечного результата умножается на соответствующий коэффициент (k_r), который характеризует индивидуальную склонность к риску ЛПР.

5.2. Графическое представление альтернатив в пространстве «Риск-доход»

Для более глубокого понимания проблемы сравнения альтернатив в условиях риска удобно представить множество анализируемых альтернатив как набор точек в двухмерном декартовом пространстве. При этом каждой альтернативе с известными ее параметрами математическим ожиданием дохода (m) и среднеквадратическим отклонением дохода (σ) соответствует точка с координатами (σ;m) в указанном пространстве (далее пространство «Риск-Доход»), причем среднеквадратическое отклонение дохода (σ) откладывается по оси абсцисс, а математическое ожидание дохода (m) – по оси ординат.

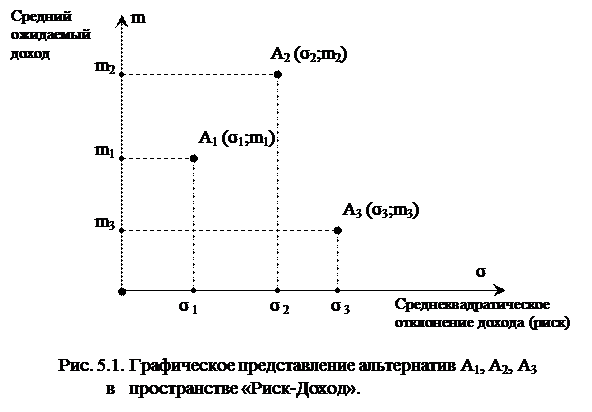Предположим, что имеются три альтернативы A₁ (σ₁;m₁), A₂ (σ₂;m₂), A₃ (σ₃;m₃), которые графически в пространстве «Риск-Доход» представлены на рис 5.1 (при допущении m₃<m₁<m₂ и σ₁<σ₂<σ₃). Для сравнения данных альтернатив необходимо формализовать отношение ЛПР к риску. Это можно сделать при помощи аппарата линий уровня, суть которого раскрыта ниже.

Проще всего проводить такой анализ для нейтральных к риску ЛПР.

Как видно на рис. 5.1., при нейтральном отношении к риску наиболее предпочтительной для ЛПР является альтернатива A₂ (σ₂;m₂), как имеющая наибольшее значение среднего ожидаемого дохода.

Допустим, отношение ЛПР к риску осторожное. В таком случае функция выбора имеет вид f_s(σ;m) = m – k_s*σ² и необходимо определить соответствующий индивидуальный коэффициент осторожности (k_s). Для этого ЛПР указывает некоторую альтернативу B(σ_а; m_а), эквивалентную A₁ (σ₁;m₁) (см. рис. 5.2.). Такая информация позволяет найти требуемый индивидуальный коэффициент осторожности к риску по представленной ранее формуле

k_s = (m₁ – m_а) / (σ₁² – σ_а²).

Зафиксировав значение функции выбора f_s(σ;m) при заданном k_s, можно получить множество точек (σ;m), представляющих в пространстве «Риск-Доход» эквивалентные друг другу альтернативы. Такие точки будут лежать на некоторой линии в указанном пространстве. Общим для них будет значение функции выбора (обозначим такое значение через K₁) Действительно, найдем показатель K₁ при известных параметрах (σ₁;m₁) из равенства:

f_s(σ₁;m₁) = m₁ – k_s·σ₁²= K₁.

Здесь K₁ – некоторая константа, отражающая «уровень» соответствующей линии в указанном пространстве при заданных параметрах (σ₁;m₁). Понятие «уровня» означает следующее. Все альтернативы, точки которых в пространстве «Риск-Доход» образуют одну кривую, эквивалентны друг другу и тем самым находятся на одном «уровне».

Далее рассмотрим указанную функцию в явном ее представлении (в пространстве «Риск-Доход»):

m = K₁+ k_s·σ²._..

Если имеют место равенства

m_i = K₁+ k_s·σ_i²,

где (m_i, σ_i) координаты некоторой i-той точки, то они представляют эквивалентные по отношению к A₁ альтернативы. Перебирая значения σ_i с некоторым шагом (пусть, например, σ₀=0, σ₁=1 и т.д.) получаем достаточное количество значений m_i, необходимых для построения кривой, отражающей множество альтернатив, эквивалентных A₁ (m₁,σ₁). Такая процедура и соответствующая кривая эквивалентности представлена на рис. 5.2. Заметим, что при i=0 имеем σ_i = σ₀ =0 и получаем:

m₀ = K₁+ k_s·σ₀² = K₁+ k_s·0² = K₁,

то есть в классе рассматриваемых функций выбора имеет место равенство K₁= m₀. Другими словами, показатель линии уровня (K₁) совпадает с ожидаемым значением (m₀) для так называемого аналога «безрискового эквивалента» анализируемой альтернативы в условиях риска.

Таким образом, удобно идентифицировать указанную кривую как линию уровня K₁, причем K₁ = m₀. Форма кривой предопределена функцией m = K₁+ k_s·σ². При положительных K₁ и k_s это парабола с ветвями вверх. При этом точка D(m₀,0) отражает эквивалентную (для точек линий уровня) «безрисковую» альтернативу, поскольку величина риска в этой точке нулевая.

Подчеркнем, что такая альтернатива называется безрисковым эквивалентом дохода для рисковых альтернатив представленных в пространстве «Риск-доход» форматом конкретной линии уровня из заданной системы линий уровня.

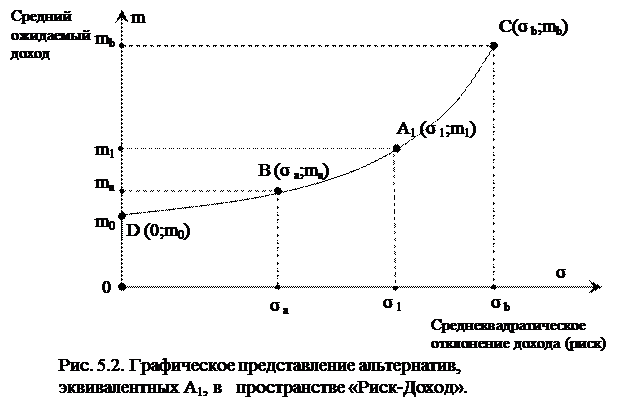Все точки, лежащие на одной кривой, эквивалентны друг другу по определению. Таким образом, под линией уровня «K» можно понимать геометрическое место точек в пространстве «Риск-Доход», эквивалентных определенной «безрисковой» альтернативе с заданным значением дохода (K = m₀). При построении соответствующего семейства линий уровня, вид которых характеризует отношение к риску, сравнение альтернатив происходит удобнее и очевиднее на основе аппарата линий уровня.

Построение линии уровня, проходящей через точку A₁^**(σ₁;m₂), требует построения функции m = K_1а+ k_s·σ², где K_1а= m₂ – k_s·σ₁². Таким образом, можно получить все необходимые кривые любых уровней.

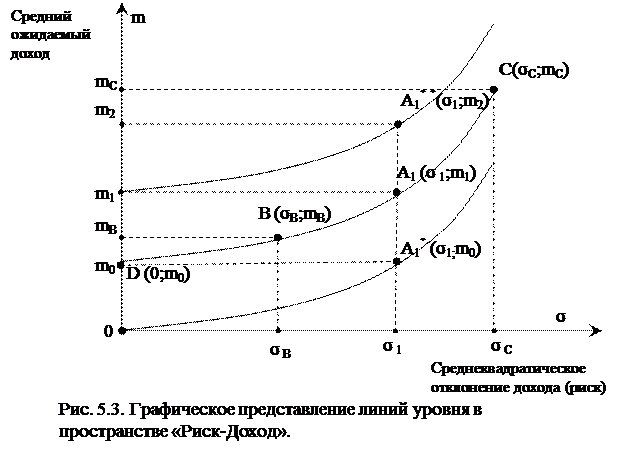На рис. 5.3 видно, что на линии уровня m₀ расположены точки D(0;m₀), B(σ_В,m_В), C(σ_С;m_С)_, которые эквивалентны исходной точке A₁ (σ₁;m₁). При этом для ЛПР более предпочтительными являются точки, лежащие на более высоких линиях уровня, представляющие альтернативы с бóльшими значениями функции выбора.

При выраженном отношении к риску на рис. 5.3 также видно, что при фиксированном σ₁ любая точка ниже A₁(σ₁;m₁) является менее предпочтительной для ЛПР и, соответственно, любая точка, расположенная выше, будет более предпочтительной, поскольку лежит на линии более высокого уровня. В частности, точка A₁^*(σ_1;m₀) однозначно менее предпочтительна, чем A₁(σ₁;m₁), поскольку лежит на линии уровня 0. Точка A₁^**(σ₁;m₂) более предпочтительна для ЛПР, чем A₁(m₁,σ₁), так как лежит на линии уровня m₁> m₀.

Очевидно также, что все точки, лежащие на прямой m = m₀ (рис. 5.3) будут заведомо менее предпочтительны, чем безрисковый эквивалент точки A₁, представленный точкой D (0;m₀), поскольку будет иметь место ненулевой риск при сохранении среднего ожидаемого дохода на прежнем уровне. Для того, чтобы достичь безрискового эквивалента, для каждой точки прямой m = m₀ необходимо такое увеличение среднего ожидаемого дохода альтернативы, которое бы компенсировало принимаемый риск. В частности, применительно к точке A₁^* (σ_1;m₀) для этого потребуется увеличение среднего ожидаемого дохода на величину m₁ – m₀.

Вернемся к задаче сравнения трех альтернатив A₁ (σ₁;m₁), A₂ (σ₂;m₂), A₃ (σ₃;m₃). Зная, что отношение осторожного к риску ЛПР в пространстве «Доход – Риск» графически определяется функцией m = K+ k_s·σ² при k_s = (m₁ – m_а) / (σ₁² – σ_а²) (см. рис. 5.2.), построим эти кривые (они будут проходить через интересующие нас точки).

Для точки A₁ (σ₁;m₁) имеем K = K₁= m₁ – k_s·σ₁²= m₀,

для точки A₂ (σ₂;m₂) имеем K = K₂= m₂ – k_s·σ₂²= m_2а,

для точки A₃ (σ₃;m₃) имеем K = K₃= m₃ – k_s·σ₃²= m_3а.

Из рис. 5.4 для анализируемой ситуации легко видеть следующее. На основе аппарата линий уровня при осторожном отношении ЛПР к риску с конкретным коэффициентом индивидуальной осторожности k_s, как видим, наиболее предпочтительной является точка A₂ (σ₂;m₂), поскольку она лежит на самой высокой линии уровня:

m_2а> m₀ > m_3а.

При склонности к риску функция выбора имеет вид f_s(σ;m) = m + k_r·σ², что определяет и явную форму соответствующих линий уровня m = K – k_r·σ². При этом, если, допустим, ЛПР сочтет альтернативы A₁ (σ₁;m₁) и A₃ (σ₃;m₃) эквивалентными, то представляющие их точки будут лежать на одной линии уровня m_1b, как показано на рис. 5.5.

Как видно на рис.5.5., наиболее предпочтительной окажется точка A₂ (σ₂;m₂) как лежащая на наивысшей линии уровня. Однако, рассуждения в общем виде дают лишь общую схему решения задачи выбора наилучшей альтернативы при заданном отношении к риску, определяющем форму линий уровня. В каждом случае решения и их точные графические представления зависят от конкретных значений параметров рассматриваемых альтернатив.