4.
Определение 1. Функция f (x) называется непрерывной в точке х0, если она удовлетворяет следующим трем условиям:
1. Функция определена в точке х0 (т.е. существует f (x0) );
2. Имеет конечный предел функции при х → х0;
3. Этот предел равен значению функции в точке х0, т.е.
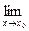 f (x) = f (x0).
f (x) = f (x0).
Определение 2. Функция у = f(х) называется непрерывной в точке х0, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
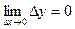 .
.
Точка х0 называется точкой разрыва функции f (x), если эта функция в данной точке не является непрерывной.
Точка разрыва является точкой разрыва первого рода, если существуют конечные односторонние пределы функции слева и справа при х → х0, не равные друг другу.
Точка разрыва является точкой разрыва второго рода, если xотя бы один из односторонниx пределов слева или справа равен бесконечности или не существует.
Свойства функций, непрерывных в точке:
1. Если функции f (х) и φ(х) непрерывны в точке х0, то иx сумма, произведение и частное (при условии φ(х0) ≠ 0 ), являются функциями, непрерывными в точке х0.
2. Если функция y = f (х) непрерывна в точке х0 и f (х0) > 0, то существует такая окрестность точки х0, в которой f (x) > 0.
3. Если функция y = f (u) непрерывна в точке u0, а функция u = φ(x) непрерывна в точке u0 = φ(x0), то сложная функция y = f 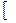 φ(x)
φ(x)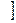 непрерывна в точке х0 .
непрерывна в точке х0 .
Свойство 3 может быть записано в виде
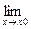 f
f 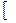 φ(x)
φ(x)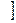 = f
= f 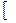
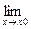 f φ(x)
f φ(x)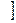 ,
,
т.е. под знаком непрерывной функции можно переходить к пределу.
Функция y = f (x) называется непрерывной на промежутке X, если она непрерывна в каждой точке этого промежутка.
Свойства функций, непрерывных на отрезке:
1. Если функция y = f (x) непрерывна на отрезке 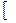 а, b
а, b 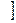 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
2. Если функция y = f (x) непрерывна на отрезке 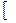 а, b
а, b 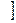 , то она достигает на этом отрезке наименьшего значения m и наибольшего значения M.
, то она достигает на этом отрезке наименьшего значения m и наибольшего значения M.
3. Если функция y = f (x) непрерывна на отрезке 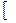 а, b
а, b 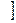 и значения ее на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка ξ є (а, b) такая, что f (ξ) = 0.
и значения ее на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка ξ є (а, b) такая, что f (ξ) = 0.
 2014-02-09
2014-02-09 653
653








