Связь между дифференцируемостью и непрерывностью

Дифференцируемость функции.

Определение. Производной функции y = f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении к нулю (если этот предел существует):

у' = = .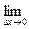

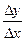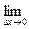
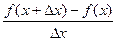Нахождение производной функции называется дифференцированием этой функции.

Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка х, называется дифференцируемой на этом промежутке.

Зависимость между непрерывностью функции и дифференцируемостью. Теорема. Если функция y = f(x) дифференцируема в точке х_o, то она в этой точке непрерывна.

Обратное не всегда верно.