Т.1.3. Производная. Основные правила и формулы дифференцирования. Геометрический, механический и экономический смысл производной, 4ч

5.

Раскрытие некоторых видов неопределённостей

Для раскрытия неопределённости вида :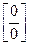

а) Можно сократить дробь на множитель, который обращает функцию в нуль;

б) Если есть иррациональность в числителе или в знаменателе, то и числитель, и знаменатель домножают на сопряженное выражение;

в) Удобно предварительно сделать замену.

Для раскрытия неопределённости :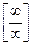

а) Если в числителе и знаменателе многочлены каких-либо степеней, то для раскрытия неопределённости делим и числитель, и знаменатель на х в наибольшей степени;

б) Если наибольшая степень числителя равна наибольшей степени знаменателя, то предел равен отношению коэффициентов при старших степенях;

в) Если наибольшая степень числителя меньше наибольшей степени знаменателя, то предел будет равен нулю;

г) Если степень числителя будет больше степени знаменателя, то предел будет равен бесконечности.

Для неопределённости 1⁰:

а) Для такого рода неопределённости всегда используется второй замечательный предел.

С.Р. 1. Первый замечательный предел.

2. Точки разрыва.

План

1.Задачи, приводящие к понятию производной.

2. Определение производной. Дифференцируемость функции.

Связь между дифференцируемостью и непрерывностью.

3.Правила и формулы дифференцирования.