Основные теоремы о пределаx
3.
Связь между бесконечно малыми и бесконечно большими величинами.
Теорема. Если функция α(x) есть бесконечно малая величина при x → x0 (x → ∞), то функция f (x) = 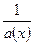 является бесконечно большой при x → x0 (x → ∞), и наоборот.
является бесконечно большой при x → x0 (x → ∞), и наоборот.
Пусть f (х) и φ(х) - функции, для которых существуют пределы при x → x0 (или при x → ∞ ): 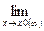 f (x) = А,
f (x) = А, 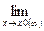 φ(x) = В.
φ(x) = В.
Основные теоремы о пределах:
1. Функция не может иметь более одного предела.
2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.
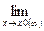
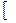 f (x)
f (x) + φ(x)
+ φ(x)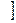 = А + В.
= А + В.
3. Предел произведения конечного числа функций равен произведению пределов этих функций, т.е.
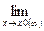
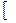 f (x)φ(x)
f (x)φ(x) = АВ.
= АВ.
4. Предел частного двух функций равен частному пределу этих функций (при условии, что предел делителя не равен нулю), т.е.
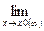
 =
= 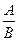 (В ≠ 0 ).
(В ≠ 0 ).
5. Если 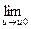 f (u) = А,
f (u) = А, 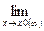 φ(x) = u0, то предел сложной функции
φ(x) = u0, то предел сложной функции
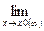 f
f 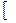 φ(x)
φ(x)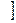 = А.
= А.
6. Если в некоторой окрестности точки x0 (или при достаточно больших х) f (x) <φ(x), то
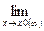 f (x)
f (x)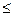
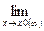 φ(x).
φ(x).
 2014-02-09
2014-02-09 1401
1401
