2.
1.
1. Задача о касательной. Путь на плоскости Оxy дана непрерывная кривая y = f (x) и необходимо найти уравнение касательной к этой кривой в точке М 0 (х0, у0).
Решение: Дадим аргументу х0 приращение Δ x и перейдем на кривой у = f (х) от точки М 0 (х0; f (х0)) к точке М 1 (x0 + Δ x; f (х0 + Δ х)). Проведём секущую М 0; М 1.
Под касательной к кривой y = f(x) в точке М 0 естественно понимать предельное положение секущей М 0 М 1 при приближении точки М 1 к точке М 0, т.е. при Δ x 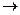 0.
0.









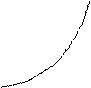 F (x0 +Δ x) M
F (x0 +Δ x) M





 F(x0) M0
F(x0) M0
 | |||
 | |||
 | |||

 α φ
α φ

х0 х0 + Δх
Уравнение прямой, проходящей через точку М 0, в соответствии имеет вид
y - f(х0) = k(х - х 0 ).
Угловой коэффициент (или тангенс угла φ наклона) секущей kM1M0 может быть найден из Δ М0М1N: kМ0M1 = tg φ = 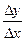 . Тогда угловой коэффициент касательной
. Тогда угловой коэффициент касательной
k = 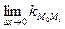 =
= 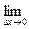
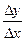 .
.
2. Задача о скорости движения. Пусть вдоль некоторой прямой движется точка по закону S = S(t), где S - пройденный путь, t - время, и необходимо найти скорость точки в момент t 0.
К моменту времени t 0 пройденный путь составит S 0 = S (t 0), а к моменту (t0+Δ t) - путь S 0 + Δ S = S (t 0 + Δ t).
Δ S
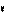
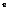
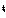
 S(t)
S(t)
t0 t0 + Δ t
Δ t
Тогда за промежуток Δ t средняя скорость будет v ср = 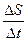 . Чем меньше Δ t, тем лучше средняя скорость характеризует движение точки в момент t 0, Поэтому под скоростью точки в момент t0 естественно понимать предел средней скорости за промежуток от t 0 до t 0 + Δ t, когда Δ t
. Чем меньше Δ t, тем лучше средняя скорость характеризует движение точки в момент t 0, Поэтому под скоростью точки в момент t0 естественно понимать предел средней скорости за промежуток от t 0 до t 0 + Δ t, когда Δ t 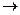 0, т.е.
0, т.е.
v = 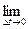 vср =
vср = 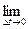
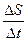 .
.
 2014-02-09
2014-02-09 607
607








