Степенно-показательная функция

Степенная функция

Теперь мы можем доказать формулу производной степенной функции у = xⁿ для любого n. Действительно In у = n In х. Дифференцируя обе части равенства, получим

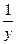у' = п · 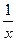, откуда у' = nу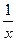= nхⁿ ·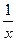= nх^n-1, т.е.

(х^п)' = nх^n-1 и (uⁿ)' = nu^n-1u'.

у = f(x) ^φ(x). Найдем In у = φ (x) In f(x). Дифференцируя, получим

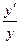= φ ' (x) In f(x) + φ (x) 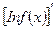= φ ' (x) In f(x) + .

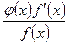Учитывая, что у = f(x) ^φ(x) получим после преобразований

у' = φ (x) f(x) ^φ(x)-1 , f'(x) + f(x)^φ(x) In f(x) φ ' (x)

Производная логарифмической функции (In у) = 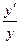называется логарифмической производной. Ее удобно использовать для нахождения производных функций, выражения которых существенно упрощаются при логарифмировании. Логарифмическую производную (In у) ' = 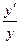называют также относительной скоростью изменения функции или темпом изменения функции.