Производные основных элементарныx функций
а) у = ех. Прологарифмируем обе части равенства по основанию е, получим In у = х. Дифференцируя обе части по переменной х и учитывая, что In у - сложная функция, получим
(In у) ' = х' или 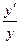 = 1, откуда у' = 1, т.е.
= 1, откуда у' = 1, т.е.
(ех)' = ех и (еu)' = еu · u'.
Заметим, что кривая с учетом у = ех, называемая экспонентой, обладает отличающим только ее свойство: в каждой точке х ординаты кривой у = ех равна угловому коэффициенту (тангенсу угла наклона) касательной к кривой в этой точке: ех = tgа.
б) у = ax.
у' = (ах)' = 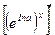 = (ех In а ) ' и по правилу дифференцирования сложной функции
= (ех In а ) ' и по правилу дифференцирования сложной функции 
у' = ех In а (х In а) ' = ах · In а. Итак,
(ах)' = ах In а и (аu)' = аu In а · u'.
 2014-02-09
2014-02-09 524
524








