Тригонометрические функции

а) y = sin x. Воспользуемся схемой нахождения производной:

1. у + Δ у = sin (x + Δ х).

2. Δ у = sin (x + Δ х) - sin x = 2sin 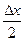cos (х + ).

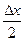3. = .

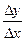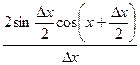4. у ' = 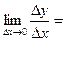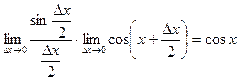(учли первый замечательный предел и непрерывность функции cos х).

Итак, (sin x) ' = cos х и (sin u) ' = cos u · u'.

б) y = cos x.

(cos х)' = -sin х и (cos u') = -sin u · u'.

(доказательство аналогично п. а).

в) у = tg х.

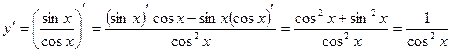, т.е.

(tgx) ' = 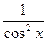и (tg 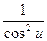u)' = · u'.

г) у = ctg x.

(ctg x) ' = -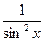; (ctg u) ' = -.

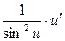(доказательство аналогично п. в).

д) у = arcsin x, где -1 ≤ х ≤ 1 и -π/2 ≤ у ≤ π/2.

Обратная функция имеет вид х = sin у, причем х'_у = cos у ≠ 0, если -π/2 < у < π/2.

Используем правило дифференцирования обратной функции

у'_х = _.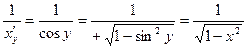

При х = ±1 производной не существует.

Итак,

(arcsin x) ' = 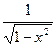и (arcsin u) ' = 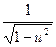· u '.

е) у = arccos x, у = arctg x, arcctg x.

(Вывод формул аналогичен п. д).

С.Р. 1. Геометрический, механический и экономический смысл производной.

2. Производная неявной функции.

3.Уравнение касательной к графику функции.