Асимптоты графика функции

3.

Определение. Асимптотой графика функции y = f(х) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(х)), до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

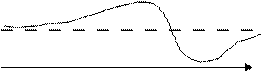
Горизонтальная Вертикальная

асимптота асимптота

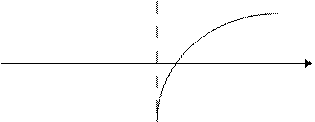Теорема 1. Пусть функция y = f(х) определена в некоторой окрестности точки х₀ и xотя бы один из пределов функции при х → х₀ – 0(слева) или при х → х₀ + 0 (справа) - равен бесконечности, т.е. 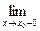f(x) = ∞ или 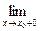f(x) = ∞. Тогда прямая х = х₀ является вертикальной асимптотой графика функции y = f(x).

Теорема 2. Пусть функция y = f(x) определена при достаточно больших х и существует конечный предел функции 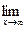f(x) = b. Тогда прямая у = b есть горизонтальная асимптота графика функции y = f(x).

Теорема 3. Пусть функция y = f(x) определена при достаточно больших х и существуют конечные пределы 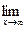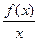= k и 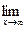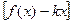= b. Тогда прямая у = kx + b является наклонной асимптотой графика функции y = f(x).