2014-02-09
524
Таблица интегралов
3.
2.
1.
Определение. Функция F(x) называется первообразной функцией для функции f(x) на промежутке X, если в каждой точке х этого промежутка F'(x) = f(x).
По геометрическому смыслу производной F'(x) есть угловой коэффициент касательной к кривой y = F(x) в точке с абсциссой х. Геометрически найти первообразную для f(x) - значит найти такую кривую y = F(x), что угловой коэффициент касательной к ней в произвольной точке х равен значению f(x) заданной функции в этой точке.
Геометрически это означает, что если найдена одна кривая y = F(x), удовлетворяющая условию F'(x) = tg a= f(x), то сдвигает её вдоль оси ординат, мы вновь получаем кривые, удовлетворяющие указанному условию.
Теорема. Если F1(x) и F2(x) - первообразные для функции f(x) в некотором промежутке X, то найдётся такое число С, что справедливо равенство
F2(x) = F1(x)+ C
Поскольку (F2(x) - F1(x))' = F2'(x) - F'1(x) = f(x) - f(x) = 0, то, по следствию из теоремы Лагранжа, найдется такое число С, что F2(x) - F1(x) = С или F2(x) = F1(x) + С.
Из данной теоремы следует, что, если F(x) - первообразная для функции f(x), то выражение вида F(x) + С, где С - произвольное число, задает все возможные первообразныедля f(x).
Определение. Совокупность всеx первообразных для функции f(x) на промежутке X называется неопределённым интегралом от функции f(x) и обозначается ∫ f(x)dx, где ∫ - знак интеграла, f(x) - подынтегральная функция, f(x)dx - подынтегральное выражение. Таким образом,
∫ f(x)dx = F(x)+C,
где F(x) - некоторая первообразная для f(x), C - произвольная постоянная.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
Свойства неопределённого интеграла
Рассмотрим основные свойства неопределенного интеграла.
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е.
(∫ f(x) dx)' = f(x).
2. Дифференциал неопределённого интеграла равен подынтегральному выражению, т.е.
d (∫ f(x) dx) = f(x)dx.
3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
∫ dF(x) = F(x) + С.
4. Постоянный множитель можно выносить за знак интеграла, т.е.
∫ а f(x) dx =а ∫ f(x) dx.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этиx функций, т.е.
∫ (f(x) ± g(x))dx = ∫ f(x)dx ± ∫ g(x)dx.
Интегралы от элементарныx функций называются табличными.
1. ∫ 0 dx = С,
2. ∫ x ndx =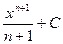 
, n ≠ -1,
3. ∫
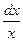= In | x | + C,
4. ∫ axdx =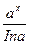 
+ C, a > 0, a ≠ 1,
5. ∫ exdx = ex + C,
6. ∫ sin x dx = -cos x + C,
7. ∫ cos x dx = sin x + C,
8. ∫
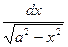= arcsin
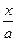+ C, -a < x < a, a > 0,
9. ∫
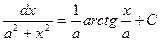, a ≠ 0,
10. ∫
= 
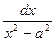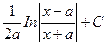, a ≠ 0,
11. ∫
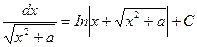, a ≠ 0.
С.Р. 1. Неберущиеся интегралы.
2.Вывод формул из таблицы интегралов.
План
1.Метод разложения.
2.Метод подстановки.
3.Метод интегрирования по частям.
