1. Уравнение вида
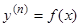 (6)
(6)
легко интегрируется в квадратурах. В самом деле, из этого уравнения последовательным интегрированием получаем:
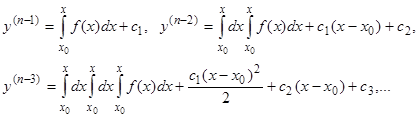
и, наконец,
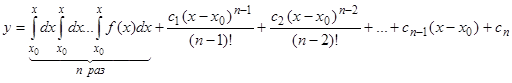 . (7)
. (7)
Формула (7) дает общее решение уравнения (6). При этом из промежуточных формул очевидно, что формула (7) представляет собой решение такой задачи Коши: найти решение уравнения (6), удовлетворяющее начальным данным: при 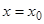
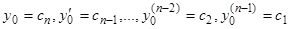 . Следовательно, первое слагаемое правой части в формуле (7)
. Следовательно, первое слагаемое правой части в формуле (7)
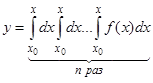 (8)
(8)
представляет собой частное решение уравнения (6), которое вместе со своими производными до 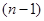 -го порядка обращается в нуль при
-го порядка обращается в нуль при 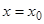 .
.
Это выражение (8), содержащее  -кратную квадратуру по
-кратную квадратуру по  , может быть преобразовано к такому виду, где содержится только одна квадратура по параметру.
, может быть преобразовано к такому виду, где содержится только одна квадратура по параметру.
Начнем со случая 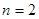 . Обозначая для большей ясности переменные интегрирования в двух интегралах разными буквами, имеем
. Обозначая для большей ясности переменные интегрирования в двух интегралах разными буквами, имеем 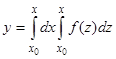 . Рассматривая правую часть последнего выражения как двойной интеграл в плоскости
. Рассматривая правую часть последнего выражения как двойной интеграл в плоскости 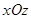 , мы видим, что он распространен на площадь заштрихованного треугольника. Мы можем изменить порядок интегрирования, взяв пределы по
, мы видим, что он распространен на площадь заштрихованного треугольника. Мы можем изменить порядок интегрирования, взяв пределы по  от
от 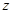 до
до  , а по
, а по 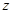 — от
— от 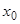 до
до  (формула Дирихле); тогда получим
(формула Дирихле); тогда получим 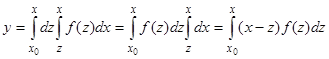 .
.
Рассмотрим далее случай 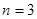 :
: 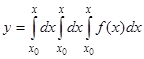 . Так же, как и раньше, два внутренних интегрирования мы можем заменить одним по параметру
. Так же, как и раньше, два внутренних интегрирования мы можем заменить одним по параметру 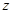 , т.е. написать
, т.е. написать 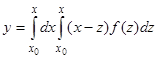 . Интегрирование опять распространяется на тот же треугольник плоскости
. Интегрирование опять распространяется на тот же треугольник плоскости 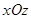 . Меняя порядок интегрирования и изменяя пределы, находим
. Меняя порядок интегрирования и изменяя пределы, находим
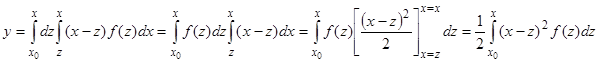 .
.
Переходим к любому  ; допустим, что для
; допустим, что для 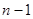 справедлива формула
справедлива формула
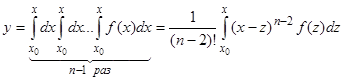 .
.
Тогда получаем:
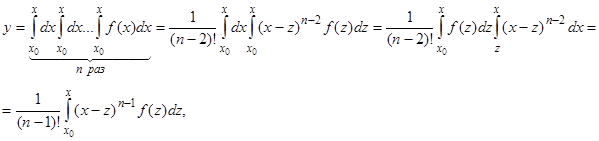
т.е. та же формула справедлива для  . Итак, окончательно имеем для всякого натурального
. Итак, окончательно имеем для всякого натурального  :
:
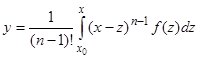 — (8.1)
— (8.1)
формула Коши (сведения  -кратного интеграла к интегралу, содержащему одно интегрирование). Формула (8.1) представляет собой решение уравнения (6), удовлетворяющее начальным условиям
-кратного интеграла к интегралу, содержащему одно интегрирование). Формула (8.1) представляет собой решение уравнения (6), удовлетворяющее начальным условиям 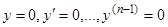 при
при 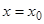 . Дифференцированием можно убедиться в справедливости обоих этих утверждений.
. Дифференцированием можно убедиться в справедливости обоих этих утверждений.
Пример. 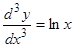 ; начальные значения
; начальные значения 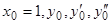 — любые числа. Тогда
— любые числа. Тогда 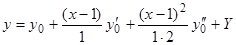 , где
, где 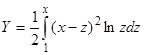 .
.
Интегрируя по частям, находим:
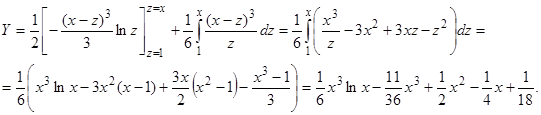
Мы получили, таким образом, частное решение, удовлетворяющее начальным условиям 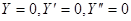 при
при 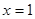 . Чтобы получить искомое общее решение, связанное с задачей Коши, мы должны прибавить квадратный трехчлен относительно
. Чтобы получить искомое общее решение, связанное с задачей Коши, мы должны прибавить квадратный трехчлен относительно 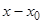 . Получим
. Получим
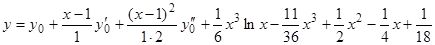 .
.
Если мы просто желаем получить общее решение (содержащее три произвольные постоянные), то достаточно заметить, что в силу произвола выбора значений 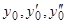 коэффициенты при
коэффициенты при 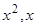 и свободный член в последнем выражении являются совершенно произвольными, и мы можем написать искомое общее решение в виде
и свободный член в последнем выражении являются совершенно произвольными, и мы можем написать искомое общее решение в виде 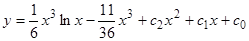 ,
, 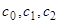 — произвольные постоянные.
— произвольные постоянные.
Если дано уравнение вида
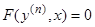 , (6.1)
, (6.1)
то, разрешив его относительно 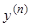 , мы приведем его к виду (6), и все предыдущие рассуждения сохраняют силу. Но иногда удается разрешить это уравнение в элементарных функциях лишь относительно
, мы приведем его к виду (6), и все предыдущие рассуждения сохраняют силу. Но иногда удается разрешить это уравнение в элементарных функциях лишь относительно  или, в более общем случае, выразить
или, в более общем случае, выразить  и
и 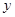 как функции параметра
как функции параметра 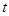 . Тогда интегрирование уравнения (6.1) может быть тоже сведено к квадратурам, выраженным явно. Пусть параметрические уравнения, эквивалентные уравнению (6.1), выглядят как
. Тогда интегрирование уравнения (6.1) может быть тоже сведено к квадратурам, выраженным явно. Пусть параметрические уравнения, эквивалентные уравнению (6.1), выглядят как
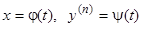 . (6.2)
. (6.2)
По определению, 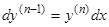 , или, в наших условиях,
, или, в наших условиях, 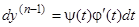 , откуда
, откуда 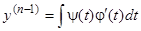 . Далее,
. Далее, 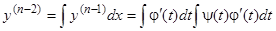 и т.д. Здесь мы не пишем произвольных постоянных, включая их в знак неопределенного интеграла. Если написать их явно, то, например, в выражении для
и т.д. Здесь мы не пишем произвольных постоянных, включая их в знак неопределенного интеграла. Если написать их явно, то, например, в выражении для 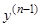 появится слагаемое
появится слагаемое 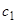 ; в выражении для
; в выражении для 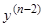 — слагаемые
— слагаемые 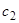 и
и 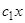 или
или 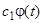 и т.д.
и т.д.
В результате получим 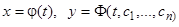 . Если из этих двух соотношений исключить
. Если из этих двух соотношений исключить 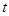 , получим общий интеграл уравнения (6.1).
, получим общий интеграл уравнения (6.1).
Пример. 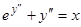 . Здесь разрешение относительно
. Здесь разрешение относительно 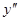 в элементарных функциях невозможно. За параметр
в элементарных функциях невозможно. За параметр 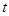 естественно взять
естественно взять 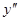 , и мы получаем параметрические уравнения:
, и мы получаем параметрические уравнения: 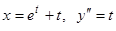 . Отсюда
. Отсюда 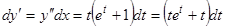 ,
, 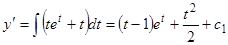 . Далее
. Далее 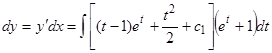 ,
, 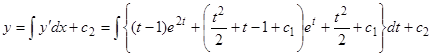 ,
,
или 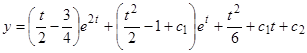 .
.
Последняя формула вместе с выражением для  ,
, 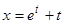 , дает параметрическое представление общего решения данного уравнения.
, дает параметрическое представление общего решения данного уравнения.
2. Уравнение вида
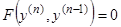 (9)
(9)
приводится к квадратурам при любом натуральном  .
.
Предположим сначала, что уравнение (9) разрешено относительно 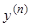 :
:
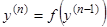 . (9.1)
. (9.1)
Вводим новую функцию 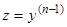 ; уравнение (9.1) примет вид
; уравнение (9.1) примет вид 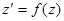 . Из этого уравнения получаем с помощью разделения переменных его общий интеграл
. Из этого уравнения получаем с помощью разделения переменных его общий интеграл 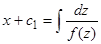 . Допустим, что это соотношение разрешено относительно
. Допустим, что это соотношение разрешено относительно 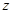 :
: 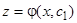 . Заменяя
. Заменяя 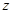 его значением
его значением 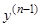 , получим уравнение
, получим уравнение 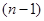 -го порядка
-го порядка 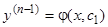 , которое мы только что рассмотрели в п.1. При его интегрировании появятся еще
, которое мы только что рассмотрели в п.1. При его интегрировании появятся еще 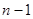 произвольных постоянных, и мы получим общее решение уравнения (9) в виде
произвольных постоянных, и мы получим общее решение уравнения (9) в виде
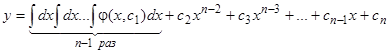 .
.
Если уравнение (9) неразрешимо в элементарных функциях относительно 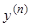 , но мы имеем выражения
, но мы имеем выражения 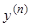 и
и 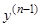 через параметр
через параметр 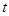 :
:
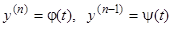 , (9.2)
, (9.2)
то соотношение 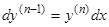 , или
, или 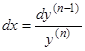 , дает нам
, дает нам 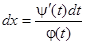 , откуда
, откуда  получается квадратурой
получается квадратурой 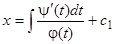 . Далее находим последовательно
. Далее находим последовательно
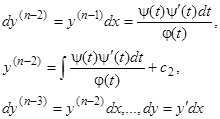
и наконец 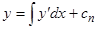 ,
,
т.е. опять представление 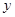 и
и  в функциях параметра
в функциях параметра 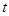 и
и  произвольных постоянных
произвольных постоянных 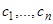 , следовательно, общее решение.
, следовательно, общее решение.
Пример. 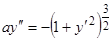 . Согласно рассмотренной теории, полагая
. Согласно рассмотренной теории, полагая 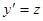 , получаем уравнение первого порядка
, получаем уравнение первого порядка 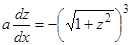 , или
, или 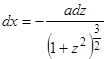 , откуда
, откуда 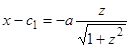 . Дальше удобно интегрировать в параметрическом виде:
. Дальше удобно интегрировать в параметрическом виде: 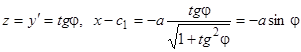 . Отсюда находим:
. Отсюда находим: 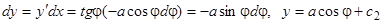 . Исключая параметр
. Исключая параметр 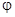 , получаем общий интеграл:
, получаем общий интеграл: 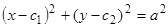 , представляющий собой уравнение семейства всех окружностей радиуса
, представляющий собой уравнение семейства всех окружностей радиуса 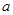 на плоскости.
на плоскости.
3. Уравнения вида
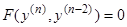 (10)
(10)
также интегрируются в квадратурах. Введение новой переменной 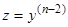 приводит уравнение (10) к уравнению второго порядка
приводит уравнение (10) к уравнению второго порядка
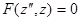 . (11)
. (11)
Если уравнение (11) разрешено относительно 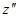 , т.е. имеет вид
, т.е. имеет вид
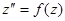 , (11.1)
, (11.1)
то один из методов его интегрирования таков: умножив обе части на 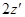 , получаем
, получаем 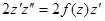 , или в дифференциалах
, или в дифференциалах 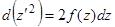 , откуда
, откуда 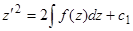 . Последнее уравнение можно разрешить относительно производной и разделить переменные:
. Последнее уравнение можно разрешить относительно производной и разделить переменные: 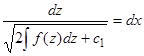 , откуда находим общий интеграл уравнения (11.1):
, откуда находим общий интеграл уравнения (11.1): 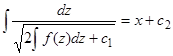 . Этот интеграл при обратной замене
. Этот интеграл при обратной замене 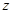 на
на 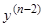 получает вид
получает вид 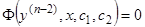 , т.е. уравнение вида (6.1). Это уравнение мы уже умеем интегрировать, интегрируется оно в квадратурах, причем это интегрирование дает еще
, т.е. уравнение вида (6.1). Это уравнение мы уже умеем интегрировать, интегрируется оно в квадратурах, причем это интегрирование дает еще 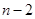 произвольных постоянных, и мы получим общее решение уравнения (10).
произвольных постоянных, и мы получим общее решение уравнения (10).
Если уравнение (10) дано в неразрешенном относительно 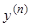 виде, но известно его параметрическое представление
виде, но известно его параметрическое представление
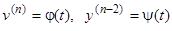 , (10.1)
, (10.1)
то интегрирование выполняется следующим образом. Мы имеем два равенства: 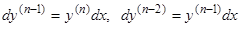 , связывающих две неизвестные функции от
, связывающих две неизвестные функции от 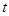 , а именно —
, а именно —  и
и 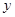 . Исключая делением
. Исключая делением 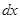 , получаем дифференциальное уравнение для
, получаем дифференциальное уравнение для 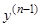 :
: 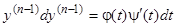 , откуда квадратурой находим
, откуда квадратурой находим 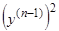 ; далее получим
; далее получим 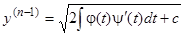 . Имея параметрическое представление
. Имея параметрическое представление 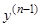 и
и 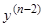 , мы свели задачу к типу (10.2), рассмотренному ранее. Дальнейшие квадратуры дадут
, мы свели задачу к типу (10.2), рассмотренному ранее. Дальнейшие квадратуры дадут 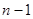 новых произвольных постоянных.
новых произвольных постоянных.
Пример. 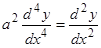 . Полагая
. Полагая 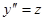 , приходим к уравнению
, приходим к уравнению 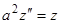 . Умножим обе части на
. Умножим обе части на 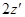 :
: 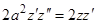 , или
, или 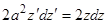 . Интегрируя, находим
. Интегрируя, находим 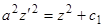 , откуда
, откуда 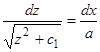 . Второе интегрирование дает
. Второе интегрирование дает 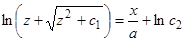 , или
, или 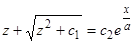 .
.
Чтобы разрешить последнее уравнение относительно 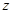 , выгодно поступить следующим образом: делим единицу на обе части последнего равенства
, выгодно поступить следующим образом: делим единицу на обе части последнего равенства 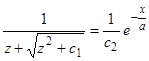 , в левой части освобождаемся от иррациональности в знаменателе, а затем умножаем обе части на
, в левой части освобождаемся от иррациональности в знаменателе, а затем умножаем обе части на 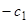 . Получаем
. Получаем 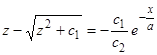 . Складывая это уравнение с исходным и деля на 2, получаем
. Складывая это уравнение с исходным и деля на 2, получаем 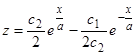 . Подставляя вместо
. Подставляя вместо 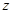 его значение
его значение 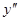 и интегрируя два раза, находим
и интегрируя два раза, находим 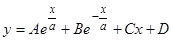 , где
, где 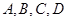 — произвольные постоянные.
— произвольные постоянные.
 2014-02-17
2014-02-17 1980
1980
