Общая теория линейных дифференциальных уравнений

Лекция 9

Линейным дифференциальным уравнением 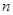-го порядка называется уравнение, линейное относительно неизвестной функции и ее производных и, следовательно, имеющее вид

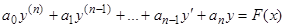, (1)

где коэффициенты 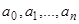(так же как и 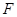) являются заданными непрерывными функциями от 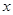(в частности, они могут быть постоянными или нулями). Если уравнение имеет порядок 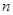, то, естественно, коэффициент 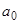не должен быть тождественно равен нулю. Допустим, что для значений 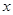в интервале

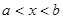(2)

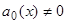и что все остальные коэффициенты и 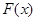непрерывны в этом интервале. Разделив обе части уравнения на 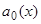и введя обозначения 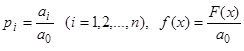, мы приведем уравнение (1) к виду

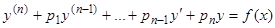, (1.1)

где 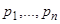и 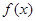— известные непрерывные функции от 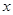. В дальнейшем будем преимущественно рассматривать линейное уравнение, приведенное к виду (1.1).

Уравнение (1) или (1.1) называется линейным неоднородным уравнением или уравнением с правой частью. Если же правая часть (или свободный член) уравнения, 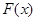или 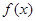, тождественно равен нулю, то уравнение называется линейным однородным:

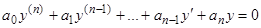, (3)

или

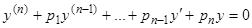. (3.1)

Если уравнение (3) или (3.1) имеет те же коэффициенты, что и (1) или (1.1), то оно называется однородным уравнением, соответствующим неоднородному уравнению (1) или (1.1).

Отметим следующие общие свойства линейных дифференциальных уравнений.

1) Уравнение остается линейным при замене независимой переменной. В самом деле, преобразуем независимую переменную подстановкой

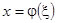, (4)

где 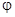есть произвольная непрерывно дифференцируемая 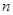раз функция, производная которой 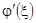не обращается в нуль в рассматриваемом интервале 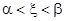, причем этот интервал соответствует изменению 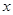в интервале (2) (это условие достаточно для существования обратной функции 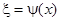, определенной в интервале (2)). Из равенства (4) имеем 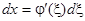. Вычисляя выражения производных от 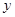по 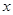через производные по новой независимой переменной, находим 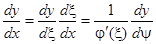, , 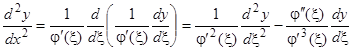… Легко видеть, что вообще 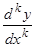выразится линейно (и однородно) через 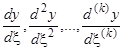, с коэффициентами — непрерывными функциями от 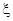. Подставляя эти выражения в уравнение (1) и производя в коэффициентах 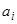и правой части 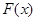замену (4), мы опять получим линейное уравнение 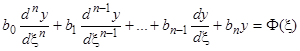, причем 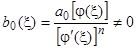в интервале 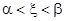. Очевидно, подстановка (4) преобразует однородное линейное уравнение снова в однородное.

2) Уравнение остается линейным при линейном преобразовании зависимой переменной. Вводим новую функцию 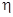, связанную с 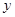уравнением

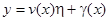, (5)

где 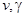имеют непрерывные производные до порядка 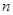включительно и 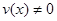в интервале (2). Мы имеем 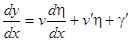, 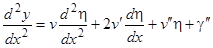. Очевидно, что вообще производная 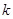-го порядка от 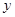по 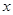выразится линейно (но неоднородно) через 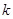первых производных от 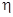по 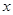. Результат подстановки этих выражений в (1) дает опять линейное уравнение. Его коэффициент при старшей производной 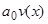, в силу сделанных предположений, не обращается в нуль в интервале (2).