Обозначим через 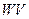 множество линейных операторов, действующих из пространства W в пространство V. На множестве
множество линейных операторов, действующих из пространства W в пространство V. На множестве 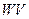 определим операции умножения оператора на скаляр
определим операции умножения оператора на скаляр 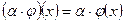 и сложение операторов
и сложение операторов 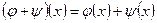 . Оператор назовем нулевым, если все векторы переводятся в ноль. Нулевой оператор обозначим через 0, т.е
. Оператор назовем нулевым, если все векторы переводятся в ноль. Нулевой оператор обозначим через 0, т.е 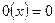 . Относительно операций умножения на скаляр и сложения множество линейных операторов
. Относительно операций умножения на скаляр и сложения множество линейных операторов 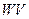 образует линейное пространство. Отметим, что
образует линейное пространство. Отметим, что 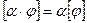 и
и 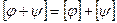 .
.
Пусть W,V,U – линейные пространства над полем P, а 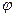 линейный оператор из W в V,
линейный оператор из W в V, 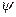 - линейный оператор из V в U. Отображение
- линейный оператор из V в U. Отображение 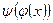 из W в U является линейным оператором и обозначается
из W в U является линейным оператором и обозначается 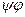 . Пусть
. Пусть 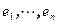 - базис W,
- базис W, 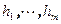 - базис V,
- базис V, 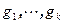 - базис U, тогда
- базис U, тогда 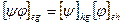 .
.
 2014-02-17
2014-02-17 1231
1231
