Планирование по конкурентной модели в краткосрочном периоде

Особенности краткосрочного периода

В рамках краткосрочного периода ограничение на ресурсы приводит к ограничению на объем выпуска 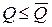, и соответствующему ограничению величины прибыли, которая может в данном случае не достигать оптимального значения; в этом случае

,

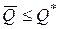и значение 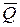, определяемое ограничением 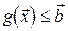(как правило, при обращении нестрогого неравенства в равенство), следует рассматривать как оптимальный объем выпуска в краткосрочном периоде.

Таким образом, если в долгосрочном периоде задача рациональной коммерческой деятельности формулировалась как задача безусловной оптимизации, то при краткосрочном планировании возникает задача на определение условного экстремума.

Оптимальный план

При краткосрочном планировании предположим, что первый ресурс ограничен величиной запаса b₁, а второй имеется в неограниченном количестве.

В этом случае формируется функция Лагранжа, которая в случае двух факторов и одного ограничения имеет вид:

,

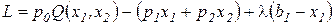и необходимые условия оптимальности записываются следующим образом:

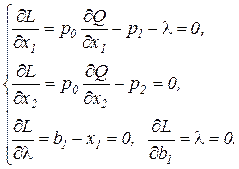
С учетом вида производственной функции Кобба-Дугласа из необходимых условий оптимальности следует:

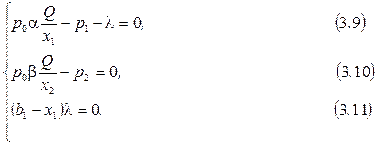
Выражения (3.9)-(3.11) являются объединением условий

,

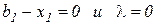поскольку они не могут выполняться совместно:

· если 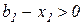, то есть 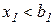, то множитель Лагранжа 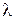показывает величину прироста дохода, который можно получить с единицы неиспользованного резерва ресурса 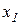; следовательно ;

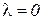· если 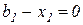, то есть ресурс 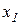использован в полном объеме, то значение 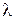может быть любым ;

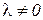· если 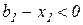, то есть 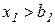, то множитель Лагранжа 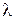представляет собой сумму снижения дохода с единицы превышения запаса ресурса, а так как превышение считается невозможным, то .

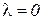Таким образом, при краткосрочном планировании возможны два случая:

§ Изменение объема выпуска до некоторой величины, ограниченной условием 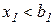, то есть из уравнения (3.9) при 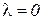и х₁=b₁,:

;

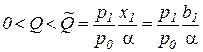в этом случае оптимальные значения факторов рассчитываются так же, как в долгосрочном периоде (так как ):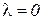

.

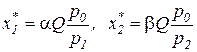§ Более значительное изменение объема выпуска, соответствующее полному исчерпанию ограниченного ресурса; в этом случае оптимальные значения равны:

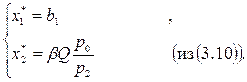(3.12)

Характерно, что при увеличении значения фиксированного ресурса (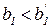) изменяется объем выпуска, соответствующий границе между долгосрочным и краткосрочным планами. Геометрическая интерпретация решения приведена на рис. 3.5.

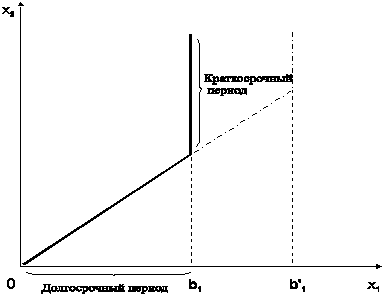Рис. 3.5. Долгосрочны и краткосрочный планы

Объем затрат второго ресурса для оптимального плана определяется из соотношения (3.12) с учетом вида производственной функции:

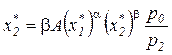, Þ ,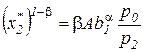

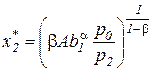. (3.13)

Поскольку показатель степени 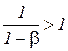, то величина затрат второго (переменного) ресурса возрастает нелинейно при увеличении соотношения цен 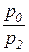, то есть чем дешевле изменяемый ресурс, тем в большем объеме он будет расходоваться для обеспечения оптимального значения объема выпуска. Кроме того, большему значению 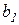ограниченного ресурса соответствуют более значительные затраты переменного ресурса (при 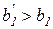на рис. 3.5).

Оптимальный объем выпуска

Оптимальный объем выпущенной продукции определяется из выражения производственной функции Кобба-Дугласа с учетом соотношения (3.12):

,

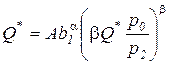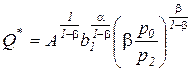. (3.14)

Поскольку в реальных производственных процессах, как было показано в работах Д. Кобба и П. Дугласа, значения показателей эластичности равны a=0,25, b=0,75, то из выражения (3.14) следуют выводы:

· оптимальный объем продукции возрастает пропорционально увеличению запаса фиксированного ресурса, так как ;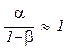

· оптимальный объем выпуска возрастает ускоренными темпами с увеличением соотношения цен продукта и переменного ресурса, так как ;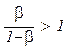

· значение оптимального объема выпуска не зависит от цены фиксированного ресурса.

Пример 3.4.1. Решить пример 3.3.1, если поставки зерна ограничены объемом 400 тонн в год. а) 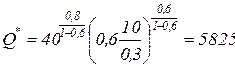тыс. тонн; б) 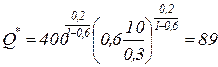тонн; в) 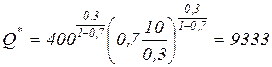тонн;

Во всех случаях оптимальный объем выпуска снизился.