Основные понятия и определения. Дифференциальные уравнения второго порядка

Дифференциальные уравнения второго порядка

Определение 1. Обыкновенным дифференциальным уравнением второго порядка называют соотношение вида:

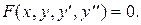(1)

Уравнение вида

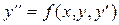(2)

называется дифференциальным уравнением второго порядка, разрешенным относительно старшей производной.

Задача Коши для дифференциального уравнения второго порядка ставится так:

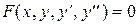
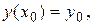(3)

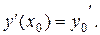(4)

Здесь 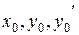- заданные числа, которые называются начальными данными.

Геометрический смысл задачи Коши (1), (3), (4) состоит в нахождении решения 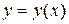уравнения (1), график которого проходит через данную точку 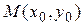и касательная к графику решения в точке 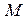имеет заданный коэффициент наклона .

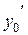Теорема существования и единственности для задачи Коши (2), (3), (4) формулируется аналогично соответствующей теореме для уравнения первого порядка.

Пусть 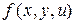есть функция трех переменных, соответствующая правой части уравнения (2).

Теорема. Если функции 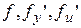непрерывны в некоторой области 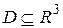, то для любой точки 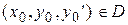задача Коши (2), (3), (4) имеет единственное решение 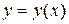, определенное в некоторой окрестности точки .

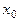Единственность решения понимается в том же смысле как для уравнения 1^го порядка.